Advertisements
Advertisements
प्रश्न
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
पर्याय
DF = 5cm, ∠F = 60°
DE = 5cm, ∠E = 60°
DF = 5cm, ∠E = 60°
DE = 5cm, ∠D = 40°
उत्तर
It is given that ΔABC \[\cong\] ΔFDE and AB = 5 CM . ∠B = 40 , and ∠A = 80°
So AB = FD and ∠C = ∠E
Now, in triangle ABC,
∠A +∠B +∠C = 180°
⇒ 80 + 40 + ∠C = 180°
⇒ ∠C = 60°
Therefore,
DF = 5cm, ∠E = 60°
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠E
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
Mark the correct alternative in each of the following:
If ABC ≅ ΔLKM, then side of ΔLKM equal to side AC of ΔABC is
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: ΔAMC≅ ΔANB

In the figure, ∠CPD = ∠BPD and AD is the bisector of ∠BAC. Prove that ΔCAP ≅ ΔBAP and CP = BP.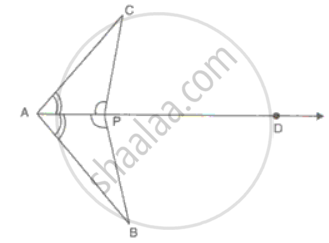
If the perpendicular bisector of the sides of a triangle PQR meet at I, then prove that the line joining from P, Q, R to I are equal.
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.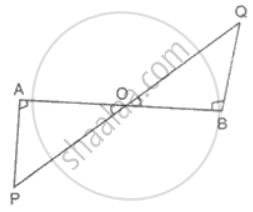
In ΔABC, AB = AC, BM and Cn are perpendiculars on AC and AB respectively. Prove that BM = CN.
∆ABC and ∆PQR are congruent under the correspondence:
ABC ↔ RQP
Write the parts of ∆ABC that correspond to
(i) `bar"PQ"`
(ii)∠Q
(iii) `bar"RP"`
The top and bottom faces of a kaleidoscope are congruent.
