Advertisements
Advertisements
प्रश्न
If the perpendicular bisector of the sides of a triangle PQR meet at I, then prove that the line joining from P, Q, R to I are equal.
उत्तर
Given:
In ΔPQR,
PA is the perpendicular bisector of QR ⇒ QA = RA
RC is the perpendicular bisector of PQ ⇒ PC = QC
QB is the perpendicular bisector of PR ⇒ PR = RB
PA, RC and QB meet at I.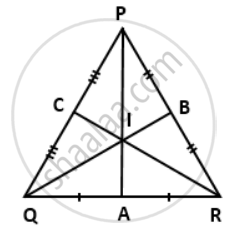
To prove: IP = IQ = IR
Proof:
In ΔQIA and ΔRIA
QA = RA ....[Given]
∠QAI = ∠RAI ....[Each = 90]
IA = IA ....[Common]
∴ By Side-Angle-Side criterion of congruence,
ΔIQ = IR ....(i)
Similarly, in ΔRIB and ΔPIB
RB = PB ...[Given]
∠RBI = ∠PBI ...[Each = 90°]
IB = IB ...[Common]
∴ By Side-Angle-Side criterion of congruence,
ΔRIB ≅ ΔPIB
The corresponding parts of the congruent triangles are congruent.
∴ IR = IP ....(ii)
From (i) and (ii), we have
IP = IQ = IR.
APPEARS IN
संबंधित प्रश्न
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the othe Prove that the triangles are congruent.
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
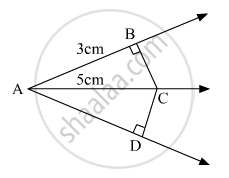
In the given figure, if AC is bisector of ∠BAD such that AB = 3 cm and AC = 5 cm, then CD =
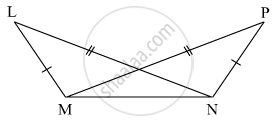
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
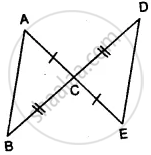
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: ΔAMC≅ ΔANB

In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 70°,BC = 6cm,∠C = 50°);
ΔXYZ;(∠Z = 60°,XY = 6cm,∠X = 70°).
In the given figure P is a midpoint of chord AB of the circle O. prove that OP ^ AB.
Two right-angled triangles ABC and ADC have the same base AC. If BC = DC, prove that AC bisects ∠BCD.
If AB = QR, BC = PR and CA = PQ, then ______.
