Advertisements
Advertisements
प्रश्न
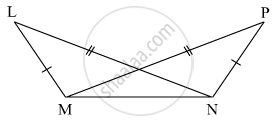
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
उत्तर
In △LMN and △PNM
seg LM ≅ seg PN
seg LN ≅ seg PM ...(Given)
seg MN ≅ seg NM ...(Common side)
△LMN ≅ △PNM ...(SSS test)
`{:("∠LMN ≅ ∠PNM"), ("∠MLN ≅ ∠NPM"), ("∠LNM ≅ ∠PMN"):} } ...("c.a.c.t.")`
APPEARS IN
संबंधित प्रश्न
If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the Corresponding congruent parts of the triangles.
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that:
State, whether the pairs of triangles given in the following figures are congruent or not:

ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.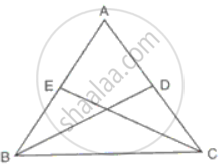
O is any point in the ΔABC such that the perpendicular drawn from O on AB and AC are equal. Prove that OA is the bisector of ∠BAC.
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.
The top and bottom faces of a kaleidoscope are congruent.
