Balbharati solutions for Geometry (Mathematics 2) [English] 9 Standard Maharashtra State Board chapter 3 - Triangles [Latest edition]

In the given figure, ∠ACD is an exterior angle of ΔABC. ∠B = 40°, ∠A = 70°. Find the measure of ∠ACD.

In ΔPQR, ∠P = 70°, ∠Q = 65° then find ∠R. 

The measures of angles of a triangle are x°, (x - 20)°, (x - 40)°. Find the measure of each angle. 

The measure of one of the angles of a triangle is twice the measure of its smallest angle and the measure of the other is thrice the measure of the smallest angle. Find the measures of the three angles.

In the given figure, measures of some angles are given. Using the measures find the values of x, y, z. 

In the given figure, line AB || line DE. Find the measures of ∠DRE and ∠ARE using given measures of some angles. 

In Δ ABC, bisectors of ∠A and ∠B intersect at point O. If ∠C = 70°. Find the measure of ∠AOB. 

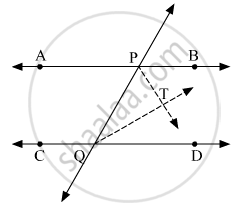
In the given Figure, line AB || line CD and line PQ is the transversal. Ray PT and ray QT are bisectors of ∠BPQ and ∠PQD respectively. Prove that m∠PTQ = 90°.

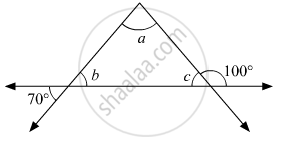
Using the information shown in figure, find the measures of ∠a, ∠b and ∠c.

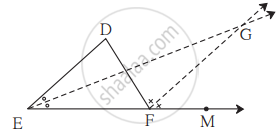
In the given figure, line DE || line GF, ray EG and ray FG are bisectors of ∠DEF and ∠DFM respectively. Prove that, 

1. ∠DEG = `1/2∠"EDF"`
2. EF = FG

In the following example, a pair of triangles is shown. Equal parts of triangles in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

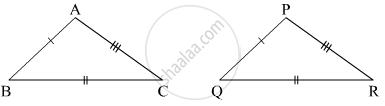
By ______ test

Δ ABC  ≅  ΔPQR

In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

 By ______ test

ΔXYZ ≅ ΔLMN

In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangles in each pair are congruent.

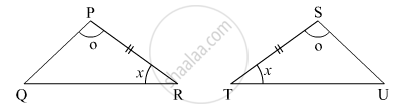
 By ______ test

ΔPRQ ≅ ΔSTU

In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

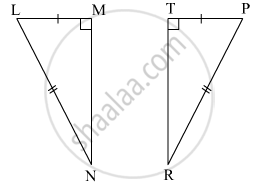
By ______ test

ΔLMN ≅ ΔPTR

Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.

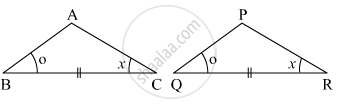
From the information shown in the figure,

In ΔABC and ΔPQR

∠ABC ≅ ∠PQR

seg BC ≅ seg QR

∠ACB ≅ ∠PRQ

∴ ΔABC ≅ ΔPQR         ...`square` test

∴ ∠BAC ≅ `square`               ...corresponding angles of congruent triangles.

`{:("seg AB" ≅ square),("and"  square ≅ "seg PR"):}}`      ...corresponding sides of congruent triangles

Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.

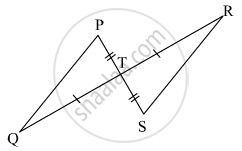
From the information shown in the figure,

in ΔPTQ and ΔSTR

seg PT ≅ seg ST

∠PTQ ≅ ∠STR        ...[Vertically opposite angles]

∴ ΔPTQ ≅ ΔSTR       ...`square` test

∴ `{:("∠TPQ" ≅ square),("and"  square ≅ "∠TRS"):}}`      ...corresponding angles of congruent triangles

seg PQ ≅ `square`         ...corresponding sides of congruent triangles

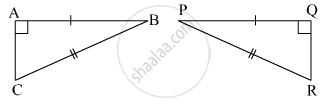
From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.

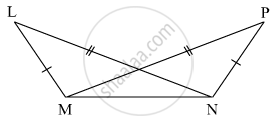
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.

In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

In the given figure, ∠P ≅ ∠R seg, PQ ≅ seg RQ. Prove that, ΔPQT ≅ ΔRQS.

Find the values of x and y using the information shown in the figure.

Find the measure of ∠ABD and m∠ACD.

The length of hypotenuse of a right angled triangle is 15. Find the length of median of its hypotenuse.

In ΔPQR, ∠Q = 90°, PQ = 12, QR = 5 and QS is a median. Find l(QS).

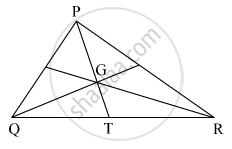
In the given figure, point G is the point of concurrence of the medians of Δ  PQR. If GT = 2.5, find the lengths of PG and PT.

In the given figure, point A is on the bisector of ∠ XYZ. If AX = 2 cm then find AZ.

In the given figure, ∠RST = 56°, seg PT ⊥ ray ST, seg PR ⊥ ray SR and seg PR ≅ seg PT. Find the measure of ∠RSP. State the reason for your answer.

In ΔPQR, PQ = 10 cm, QR = 12 cm, PR = 8 cm. Find out the greatest and the smallest angle of the triangle.

In ΔFAN, ∠F = 80, ∠A = 40°. Find out the greatest and the smallest side of the triangle. State the reason.

Prove that an equilateral triangle is equiangular.

Prove that, if the bisector of ∠BAC of ΔABC is perpendicular to side BC, then ΔABC is an isosceles triangle.

In the given figure, if seg PR ≅ seg PQ, show that seg PS > seg PQ. 

In the given figure, in ΔABC, seg AD and seg BE are altitudes, and AE = BD. Prove that seg AD ≅ seg BE.

If ΔXYZ ~ ΔLMN, write the corresponding angles of the two triangles and also write the ratios of corresponding sides.

In Δ XYZ, XY = 4 cm, YZ = 6 cm, XZ = 5 cm, If ΔXYZ ~ Δ​PQR and PQ = 8 cm then find the lengths of remaining sides of ΔPQR.

Draw a sketch of a pair of similar triangles. Label them. Show their corresponding angles by the same signs. Show the lengths of corresponding sides by numbers in proportion.

If two sides of a triangle are 5 cm and 1.5 cm, the length of its third side cannot be ______.

In ΔPQR, If ∠R > ∠Q then ______.

In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?

ΔABC is isosceles in which AB = AC. Seg BD and seg CE are medians. Show that BD = CE.

In ΔPQR, If PQ > PR and bisectors of ∠Q and ∠R intersect at S. Show that SQ > SR.

In the figure, point D and E are on side BC of ΔABC, such that BD = CE and AD = AE. Show that ΔABD ≅ ΔACE.

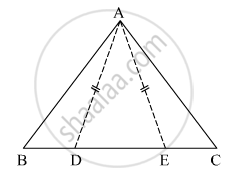
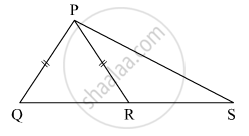
In the given figure, point S is any point on side QR of ΔPQR Prove that: PQ + QR + RP > 2PS

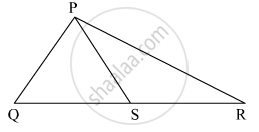
In the given figure, bisector of ∠BAC intersects side BC at point D. Prove that AB > BD.

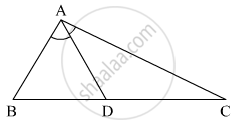
In the given figure, seg PT is the bisector of ∠QPR. A line through R intersects ray QP at point S. Prove that PS = PR.

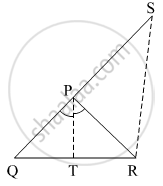
In the given figure, seg AD ⊥ seg BC. seg AE is the bisector of ∠CAB and C - E - D. Prove that ∠DAE = `1/2` (∠C - ∠B)