Advertisements
Advertisements
प्रश्न
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
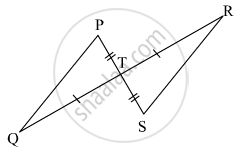
From the information shown in the figure,
in ΔPTQ and ΔSTR
seg PT ≅ seg ST
∠PTQ ≅ ∠STR ...[Vertically opposite angles]
∴ ΔPTQ ≅ ΔSTR ...`square` test
∴ `{:("∠TPQ" ≅ square),("and" square ≅ "∠TRS"):}}` ...corresponding angles of congruent triangles
seg PQ ≅ `square` ...corresponding sides of congruent triangles
उत्तर
From the information shown in the figure, in ΔPTQ and ΔSTR
seg PT ≅ seg ST
∠PTQ ≅ ∠STR ...Vertically opposite angles
∠PTQ ≅ ∠STR ...SAS test
∴ `{:("∠TPQ" ≅ bbunderline("∠TSR")),(bbunderline("∠TQP")≅ "∠TRS"):}}` ...[corresponding angles of congruent triangles]
seg PQ ≅ seg SR ...[corresponding sides of congruent triangles]
APPEARS IN
संबंधित प्रश्न
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangles in each pair are congruent.
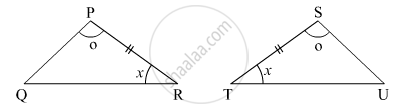
By ______ test
ΔPRQ ≅ ΔSTU
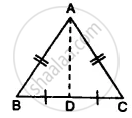
Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
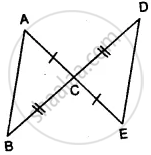
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
In the figure, AB = EF, BC = DE, AB and FE are perpendiculars on BE. Prove that ΔABD ≅ ΔFEC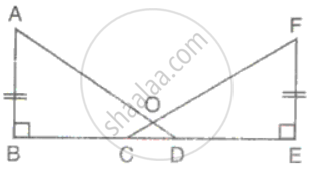
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.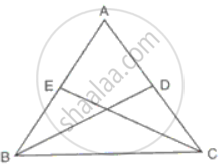
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.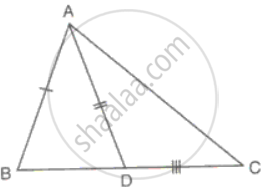
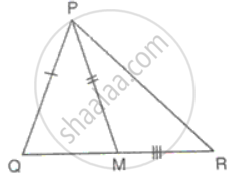
In ΔABC, AD is a median. The perpendiculars from B and C meet the line AD produced at X and Y. Prove that BX = CY.
“If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
