Advertisements
Advertisements
प्रश्न
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangles in each pair are congruent.
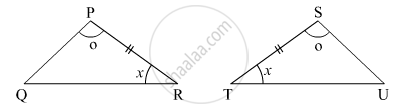
By ______ test
ΔPRQ ≅ ΔSTU
उत्तर
By ASA Test
APPEARS IN
संबंधित प्रश्न
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
If ΔABC ≅ ΔABC is isosceles with
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, BC = QR, ∠A = 90°, ∠C = ∠R = 40° and ∠Q = 50°.
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In the figure, RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.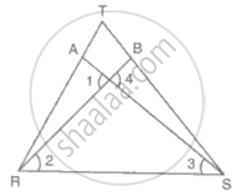
In the figure, ∠BCD = ∠ADC and ∠ACB =∠BDA. Prove that AD = BC and ∠A = ∠B.
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
