Advertisements
Advertisements
प्रश्न
In ΔABC, AD is a median. The perpendiculars from B and C meet the line AD produced at X and Y. Prove that BX = CY.
उत्तर

In ΔBXD and ΔCYD
∠BXD = ∠CYD ...(90)
∠XDB = ∠YDC ...(vertically opposite angles)
BD = DC ...(AD is median on BC)
Therefore, ΔBXD ≅ ΔCYD ...(AAS criteria)
Hence, BX = CY.
APPEARS IN
संबंधित प्रश्न
In Fig. 10.22, the sides BA and CA have been produced such that: BA = AD and CA = AE.
Prove that segment DE || BC.
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
State, whether the pairs of triangles given in the following figures are congruent or not:

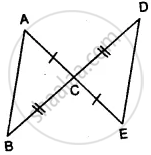
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
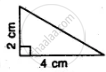
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.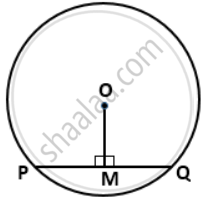
In the figure, ∠CPD = ∠BPD and AD is the bisector of ∠BAC. Prove that ΔCAP ≅ ΔBAP and CP = BP.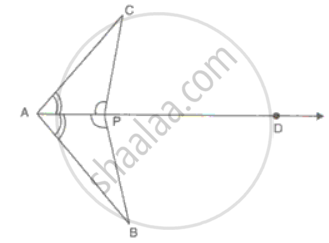
In the figure, AB = EF, BC = DE, AB and FE are perpendiculars on BE. Prove that ΔABD ≅ ΔFEC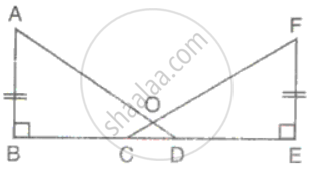
In the given figure, AB = DB and AC = DC. Find the values of x and y.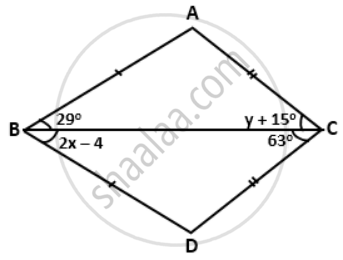
Two figures are congruent, if they have the same shape.
