Advertisements
Advertisements
प्रश्न
ΔABC is an isosceles triangle with AB = AC. GB and HC ARE perpendiculars drawn on BC.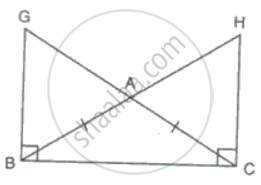
Prove that
(i) BG = CH
(ii) AG = AH
उत्तर
In ΔABC
AB = AC
∠ABC = ∠ACB ...(equal sides have equal angles opposite to them)...(i)
∠GBC = ∠HCB = 90° ........(ii)
Subtracting (i) from (ii)
∠GBA = ∠HCA..........(iii)
In ΔGBA and ΔHCA
∠GBA = ∠HCA ...(from iii)
∠BAG - ∠CAH ...(vertically opposite angles)
BC = BC
Therefore, ΔGBA ≅ ΔHCA ...(ASA criteria)
Hence, BG = CH and AG = AH.
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠E
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(EF)`
In the given figure, if AE || DC and AB = AC, the value of ∠ABD is
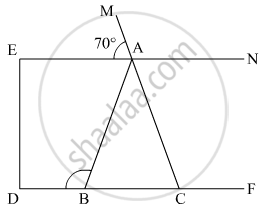
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

State, whether the pairs of triangles given in the following figures are congruent or not:

In the given figure, prove that: ∆ ABD ≅ ∆ ACD
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.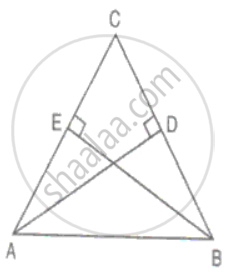
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side AB of ∆ABC so that the two triangles are congruent? Give reason for your answer.
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
