Advertisements
Advertisements
प्रश्न
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.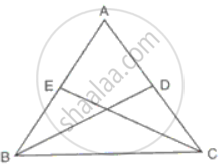
उत्तर
CE is median to AB
⇒ AE = BE ......(i)
BD is median to AC
⇒ AD = DC ......(i)
But AB =AC ......(iii)
Therefore from (i), (ii) and (iii)
BE = CD
In ΔBEC and ΔBDC
BE = CD
∠EBC = ∠DCB ...(angles opposites to equal sides are equal)
BC = BC ...(common)
Therefore, ΔBEC ≅ ΔBDC ...(SAS criteria)
Hence, BD = CE.
APPEARS IN
संबंधित प्रश्न
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
Which of the following is not a criterion for congruence of triangles?
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangles in each pair are congruent.
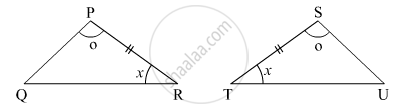
By ______ test
ΔPRQ ≅ ΔSTU
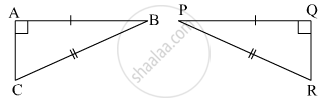
From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that: AD = CE.
State, whether the pairs of triangles given in the following figures are congruent or not:
Δ ABC in which AB = 2 cm, BC = 3.5 cm and ∠C = 80° and Δ DEF in which DE = 2 cm, DF = 3.5 cm and ∠D = 80°.
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.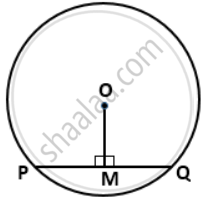
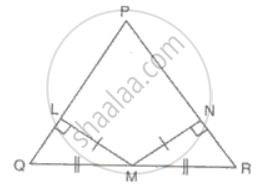
In ΔPQR, LM = MN, QM = MR and ML and MN are perpendiculars on PQ and PR respectively. Prove that PQ = PR.