Advertisements
Advertisements
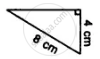
प्रश्न
Prove that:
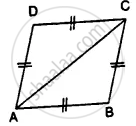
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
उत्तर
Proof:
(i) In ∆ ABC and ∆ ADC
AC = AC ...........(common)
AB = DC ............(given)
BC = AD ...........(given)
∴ ∆ ABC ≅ ∆ ADC ................(S.S.S. Axiom)
(ii) Hence ∠B = ∠D ...........(c.p.c.t.)
Hence proved.
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠E
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
In ΔPQR ≅ ΔEFD then ED =
If ΔPQR≅ ΔEFD, then ∠E =
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
State, whether the pairs of triangles given in the following figures are congruent or not:
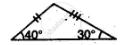
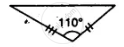
State, whether the pairs of triangles given in the following figures are congruent or not:
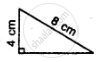
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.
Two figures are congruent, if they have the same shape.
