Advertisements
Advertisements
प्रश्न
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
उत्तर
We have to prove that ΔADE ≅ ΔBCE
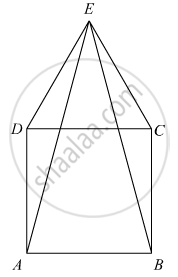
Given ABCDis a square
So AB = BC = CD = AD
Now in ΔEDC is equilateral triangle.
So DE = EC = CB
In ΔAED and ΔCEB
AD = BC (Side of triangle)
DE = CE (Side of equilateral triangle)
∠ADE = ∠ADC + ∠CDE
= 90 + 60
= 150
And,
∠BCE = ∠BCD + ∠DCE
= 90 + 60
= 150
So ∠ACE = ∠BCDE
Hence from SAS congruence ΔADE ≅ ΔBCE Proved.
APPEARS IN
संबंधित प्रश्न
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangles in each pair are congruent.
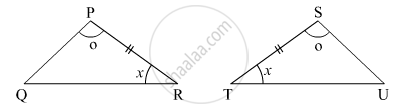
By ______ test
ΔPRQ ≅ ΔSTU
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

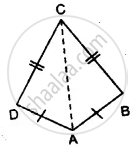
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.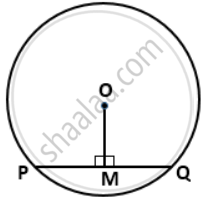
PQRS is a quadrilateral and T and U are points on PS and RS respectively such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆XYZ ≅ ∆MLN
