Advertisements
Advertisements
प्रश्न
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
उत्तर
We have to prove that ΔADE ≅ ΔBCE
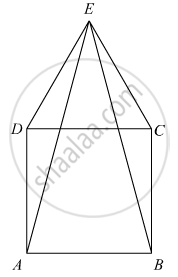
Given ABCDis a square
So AB = BC = CD = AD
Now in ΔEDC is equilateral triangle.
So DE = EC = CB
In ΔAED and ΔCEB
AD = BC (Side of triangle)
DE = CE (Side of equilateral triangle)
∠ADE = ∠ADC + ∠CDE
= 90 + 60
= 150
And,
∠BCE = ∠BCD + ∠DCE
= 90 + 60
= 150
So ∠ACE = ∠BCDE
Hence from SAS congruence ΔADE ≅ ΔBCE Proved.
APPEARS IN
संबंधित प्रश्न
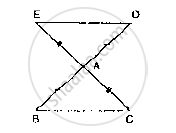
In Fig. 10.22, the sides BA and CA have been produced such that: BA = AD and CA = AE.
Prove that segment DE || BC.
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that: LN = MN.
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the othe Prove that the triangles are congruent.
In ΔPQR ≅ ΔEFD then ED =
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 70°,BC = 6cm,∠C = 50°);
ΔXYZ;(∠Z = 60°,XY = 6cm,∠X = 70°).
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
In ΔABC, AB = AC. D is a point in the interior of the triangle such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ΔABC.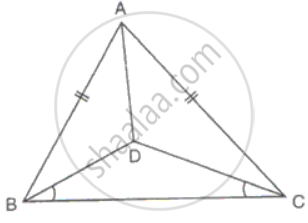
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side AB of ∆ABC so that the two triangles are congruent? Give reason for your answer.
“If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
