Advertisements
Advertisements
प्रश्न
In ΔABC, AB = AC. D is a point in the interior of the triangle such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ΔABC.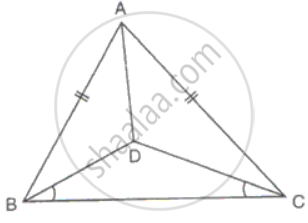
उत्तर
Since AB = AC
∠ABC = ∠ACB
But ∠DBC = ∠DBC
⇒ ∠ABD = ∠ACD
Now in ΔABD and ΔADC
AB = AC
AD = AD
∠ABD = ∠ACD
Therefore, ΔABD ≅ ΔADC ...(SSA criteria)
Hence, ∠BAD = ∠CAD
Thus, AD bisects ∠BAC.
APPEARS IN
संबंधित प्रश्न
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
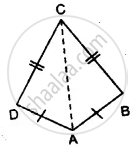
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that:
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
In the given figure P is a midpoint of chord AB of the circle O. prove that OP ^ AB.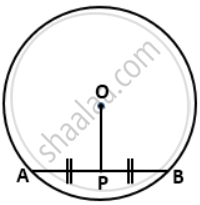
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
In ΔABC, AD is a median. The perpendiculars from B and C meet the line AD produced at X and Y. Prove that BX = CY.
In the given figure, AB = DB and AC = DC. Find the values of x and y.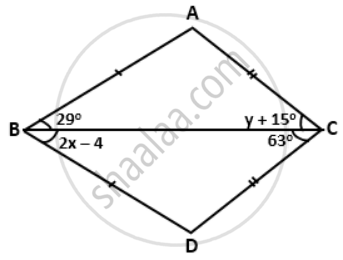
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles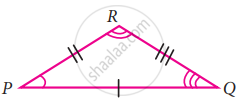
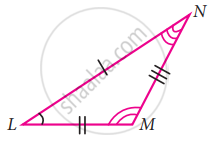
If AB = QR, BC = PR and CA = PQ, then ______.
