Advertisements
Advertisements
Question
In ΔABC, AB = AC. D is a point in the interior of the triangle such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ΔABC.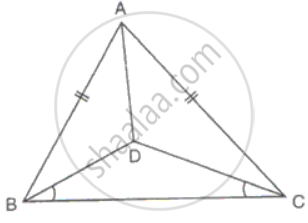
Solution
Since AB = AC
∠ABC = ∠ACB
But ∠DBC = ∠DBC
⇒ ∠ABD = ∠ACD
Now in ΔABD and ΔADC
AB = AC
AD = AD
∠ABD = ∠ACD
Therefore, ΔABD ≅ ΔADC ...(SSA criteria)
Hence, ∠BAD = ∠CAD
Thus, AD bisects ∠BAC.
APPEARS IN
RELATED QUESTIONS
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
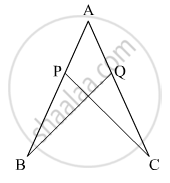
In the given figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
Which of the following is not a criterion for congruence of triangles?
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that: AD = CE.
State, whether the pairs of triangles given in the following figures are congruent or not:

In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
Two right-angled triangles ABC and ADC have the same base AC. If BC = DC, prove that AC bisects ∠BCD.
PQRS is a quadrilateral and T and U are points on PS and RS respectively such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side BC of ∆ABC so that the two triangles are congruent? Give reason for your answer.
