Advertisements
Advertisements
Question
In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
Solution
In ΔADE and ΔBAC
AE = AC
AB = AD
∠BAD = ∠EAC
∠DAC = ∠DAC = DAC ...(common)
⇒ ∠BAC = ∠EAD = EAD
Therefore, ΔADE ≅ ΔBAC ...(SAS criteria)
Hence, BC = DE.
APPEARS IN
RELATED QUESTIONS
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
In triangles ABC and PQR three equality relations between some parts are as follows:
AB = QP, ∠B = ∠P and BC = PR
State which of the congruence conditions applies:
In a ΔABC, if AB = AC and BC is produced to D such that ∠ACD = 100°, then ∠A =
State, whether the pairs of triangles given in the following figures are congruent or not:
Δ ABC in which AB = 2 cm, BC = 3.5 cm and ∠C = 80° and Δ DEF in which DE = 2 cm, DF = 3.5 cm and ∠D = 80°.
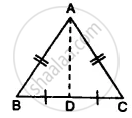
Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent sides
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles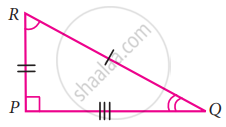

Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
