Advertisements
Advertisements
Question
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
Solution
Given:
D os mid-point of BC
⇒ BD = DC
DE = AD
To prove:
a. ΔABD ≅ ΔECD
b. AB = EC
c. AB || EC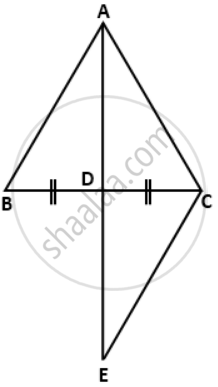
a. In ΔABD and ΔECD
BD = DC ....(given)
∠ADB = ∠CDE ....(vertically opposite angles)
AD = DE ....(given)
∴ By Side-Angle-Side criterion of congruence,
ΔABD ≅ ΔECD
b. The corresponding parts of the congruent triangle are congruent.
∴ AB = EC
c. Also, ∠DAB = ∠DEC ....(c.p.c.t)
∴ AB || EC ....(∠DAB and ∠DEC are alternate angles).
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠E
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(DF)`
In ΔPQR ≅ ΔEFD then ED =
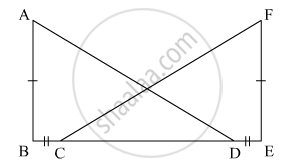
In the given figure, AB ⊥ BE and FE ⊥ BE. If BC = DE and AB = EF, then ΔABD is congruent to
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangles in each pair are congruent.
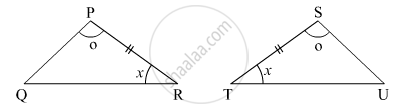
By ______ test
ΔPRQ ≅ ΔSTU
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
