Advertisements
Advertisements
Question
In the figure, ∠CPD = ∠BPD and AD is the bisector of ∠BAC. Prove that ΔCAP ≅ ΔBAP and CP = BP.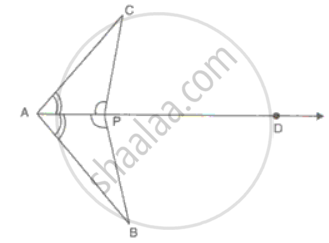
Solution
In ΔBAP and ΔCAP
∠BAP = ∠CAP ...(AD is the bisector of ∠BAC)
AP = AP
∠BPD + ∠BPA = ∠CPA + ∠CPA = 180°
∠BPD = ∠CPD
⇒ ∠BPA - ∠CPA
Therefore,
ΔCAP ≅ ΔBAP ...(ASA criteria)
Hence, CP = BP.
APPEARS IN
RELATED QUESTIONS
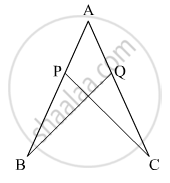
In the given figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
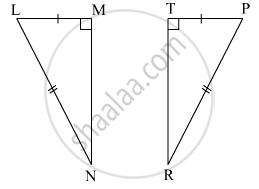
By ______ test
ΔLMN ≅ ΔPTR
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
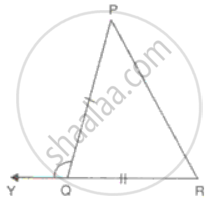
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In ΔABC and ΔPQR and, AB = PQ, BC = QR and CB and RQ are extended to X and Y respectively and ∠ABX = ∠PQY. = Prove that ΔABC ≅ ΔPQR.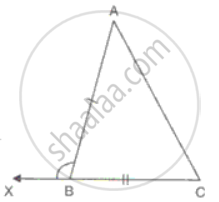
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.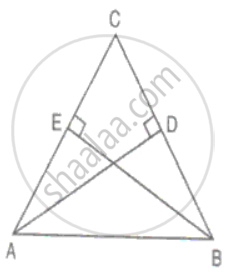
In ΔABC, AB = AC, BM and Cn are perpendiculars on AC and AB respectively. Prove that BM = CN.
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
