Advertisements
Advertisements
Question
In the figure, BC = CE and ∠1 = ∠2. Prove that ΔGCB ≅ ΔDCE.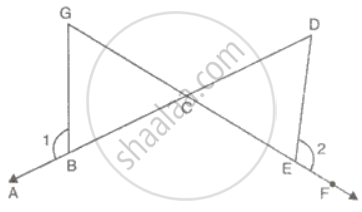
Solution
In ΔGCB and ΔDCE and
∠1 + ∠GBC = ∠2 + ∠DEC = 180°
∠1 = ∠2 =
⇒ ∠GBC = ∠DEC
BC = CE
∠GCB = ∠DCE = ...(vertically opposite angles)
Therefore,
ΔGCB ≅ ΔDCE ....(ASA criteria).
APPEARS IN
RELATED QUESTIONS
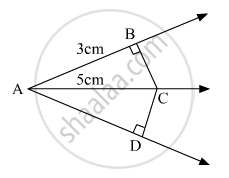
In the given figure, if AC is bisector of ∠BAD such that AB = 3 cm and AC = 5 cm, then CD =
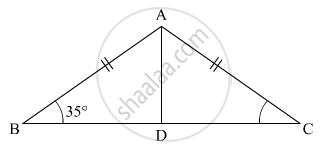
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
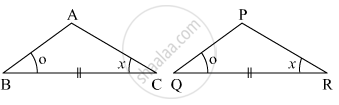
From the information shown in the figure,
In ΔABC and ΔPQR
∠ABC ≅ ∠PQR
seg BC ≅ seg QR
∠ACB ≅ ∠PRQ
∴ ΔABC ≅ ΔPQR ...`square` test
∴ ∠BAC ≅ `square` ...corresponding angles of congruent triangles.
`{:("seg AB" ≅ square),("and" square ≅ "seg PR"):}}` ...corresponding sides of congruent triangles
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that:
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 5cm,BC = 7cm,CA = 9cm);
ΔKLM;(KL = 7cm,LM = 5cm,KM = 9cm).
In ΔPQR, LM = MN, QM = MR and ML and MN are perpendiculars on PQ and PR respectively. Prove that PQ = PR.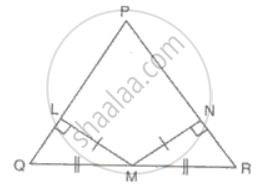
If the perpendicular bisector of the sides of a triangle PQR meet at I, then prove that the line joining from P, Q, R to I are equal.
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles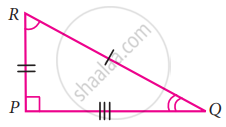

The top and bottom faces of a kaleidoscope are congruent.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆STU ≅ ∆DEF
