Advertisements
Advertisements
प्रश्न
In the figure, ∠CPD = ∠BPD and AD is the bisector of ∠BAC. Prove that ΔCAP ≅ ΔBAP and CP = BP.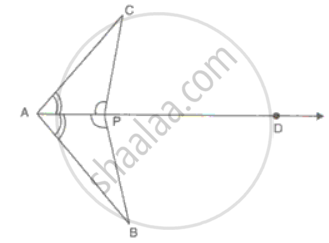
उत्तर
In ΔBAP and ΔCAP
∠BAP = ∠CAP ...(AD is the bisector of ∠BAC)
AP = AP
∠BPD + ∠BPA = ∠CPA + ∠CPA = 180°
∠BPD = ∠CPD
⇒ ∠BPA - ∠CPA
Therefore,
ΔCAP ≅ ΔBAP ...(ASA criteria)
Hence, CP = BP.
APPEARS IN
संबंधित प्रश्न
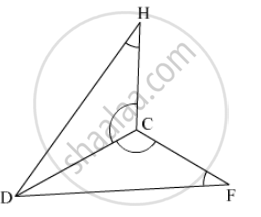
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
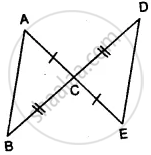
On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
State, whether the pairs of triangles given in the following figures are congruent or not:

In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
ΔABC is an isosceles triangle with AB = AC. GB and HC ARE perpendiculars drawn on BC.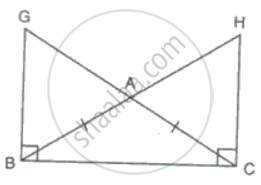
Prove that
(i) BG = CH
(ii) AG = AH
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent sides
Which of the following rule is not sufficient to verify the congruency of two triangles
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆XYZ ≅ ∆MLN
