Advertisements
Advertisements
प्रश्न
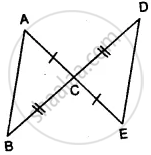
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
उत्तर
(i) In Δ ACB and Δ ECD,
AC = CE ................(given)
∠ACB = ∠DCE ............(vertically opposite angles)
BC = CD .............(given)
∴ Δ ACB ≅ Δ ECD ..............(S.A.S. Axiom)
(ii) Hence AB = ED ................(c.p.c.t.)
Hence proved.
APPEARS IN
संबंधित प्रश्न
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that: LN = MN.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
State, whether the pairs of triangles given in the following figures are congruent or not:
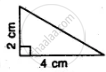

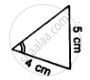
State, whether the pairs of triangles given in the following figures are congruent or not:

In the given figure P is a midpoint of chord AB of the circle O. prove that OP ^ AB.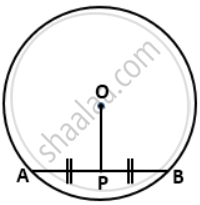
In the figure, BC = CE and ∠1 = ∠2. Prove that ΔGCB ≅ ΔDCE.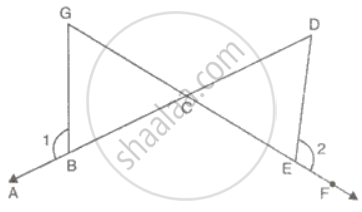
In ΔABC, X and Y are two points on AB and AC such that AX = AY. If AB = AC, prove that CX = BY.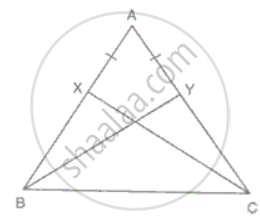
In the figure, ∠BCD = ∠ADC and ∠ACB =∠BDA. Prove that AD = BC and ∠A = ∠B.
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles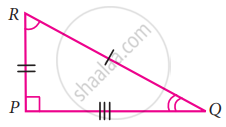

In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side AB of ∆ABC so that the two triangles are congruent? Give reason for your answer.
