Advertisements
Advertisements
प्रश्न
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles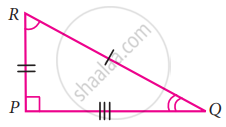

उत्तर
Given: ∆PQR ≅ ∆NML
(a) Corresponding angles
`bar("QR") = bar("LM"), bar("RP") = bar("LN"), bar("PQ") = bar("MN")`
(b) Corresponding angles
∠PQP = ∠NMN, ∠QRP = ∠MLN, ∠RPQ = ∠LNM
APPEARS IN
संबंधित प्रश्न
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the othe Prove that the triangles are congruent.
Which of the following is not a criterion for congruence of triangles?
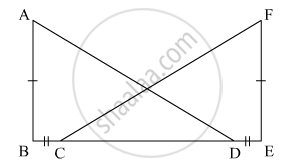
In the given figure, AB ⊥ BE and FE ⊥ BE. If BC = DE and AB = EF, then ΔABD is congruent to
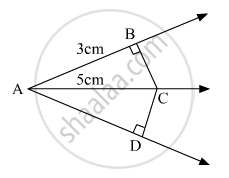
In the given figure, if AC is bisector of ∠BAD such that AB = 3 cm and AC = 5 cm, then CD =
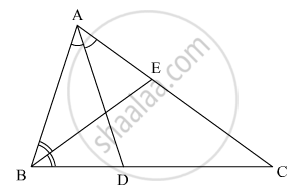
In the given figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that ADbisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
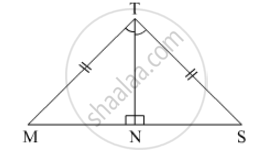
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
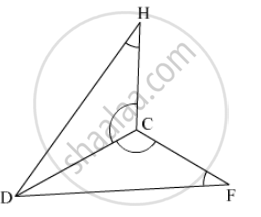
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that:
In the given figure, prove that: ∆ ABD ≅ ∆ ACD
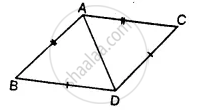
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
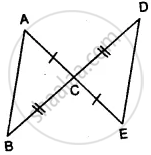
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(BC = 5cm,AC = 6cm,∠C = 80°);
ΔXYZ;(XZ = 6cm,XY = 5cm,∠X = 70°).
In the figure, ∠CPD = ∠BPD and AD is the bisector of ∠BAC. Prove that ΔCAP ≅ ΔBAP and CP = BP.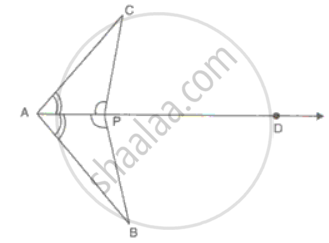
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.Prove that BO = CO and the ray AO is the bisector of angle BAC.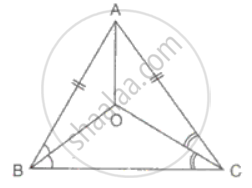
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.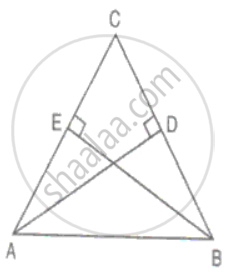
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles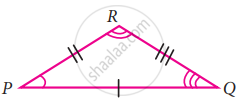
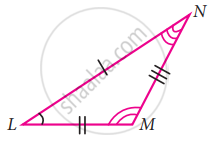
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side BC of ∆ABC so that the two triangles are congruent? Give reason for your answer.
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
