Advertisements
Advertisements
प्रश्न
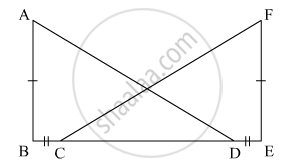
In the given figure, AB ⊥ BE and FE ⊥ BE. If BC = DE and AB = EF, then ΔABD is congruent to
विकल्प
ΔEFC
ΔECF
ΔCEF
ΔFEC
उत्तर
ΔFEC
Explanation:
It is given that
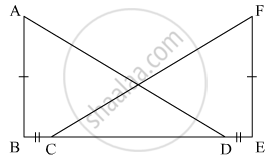
In the figure, AB ⊥ BE, FE ⊥ BE
Now, BC = DE.
Adding DC to both the sides, we get,
⇒ BC + DC = DE + DC
⇒ BD = CE
In ΔABD and ΔCEF
BD = CE (Proved)
AB = FE (Given)
∠ABD = ∠FEC (Each 90°)
∴ ΔABD ≅ ΔFEC by SAS congruence rule.
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(DF)`
Complete the congruence statement:
ΔBCA ≅?
ΔQRS ≅?
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
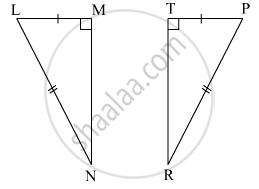
By ______ test
ΔLMN ≅ ΔPTR
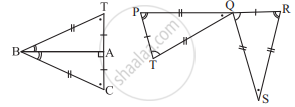
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
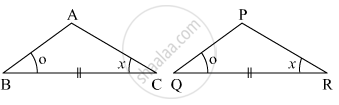
From the information shown in the figure,
In ΔABC and ΔPQR
∠ABC ≅ ∠PQR
seg BC ≅ seg QR
∠ACB ≅ ∠PRQ
∴ ΔABC ≅ ΔPQR ...`square` test
∴ ∠BAC ≅ `square` ...corresponding angles of congruent triangles.
`{:("seg AB" ≅ square),("and" square ≅ "seg PR"):}}` ...corresponding sides of congruent triangles
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: ΔAMC≅ ΔANB

State, whether the pairs of triangles given in the following figures are congruent or not:
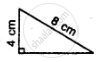
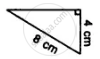
In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
