Advertisements
Advertisements
प्रश्न
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
उत्तर
In the figure, AP and BQ are equal and parallel to each other.
∴ AP = BQ and AP || BQ.
We need to prove that
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other
(i) ∵ AP || BQ
∴∠APO =∠BOQ ...[ Alternate angles ] ...(1)
and ∠PAO =∠QBO ...[ Alternate angles ] ...(2)
Now in ΔAOP and ΔBOQ.
∠APO =∠BQO ...[ from (1) ]
AP = BQ ...[ given ]
∠PAO = ∠QBO ...[ from (1) ]
∴ By Angel-Side-Angel criterion of congruence, we have
ΔAOP≅ ΔBOQ.
(ii) The corresponding parts of the congruent triangles are congruent.
∴ OP = OQ ...[ c. p. c .t ]
OA = OB ...[ c. p. c .t ]
Hence AB and PQ bisect each other.
APPEARS IN
संबंधित प्रश्न
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
If ΔABC ≅ ΔABC is isosceles with
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangles in each pair are congruent.
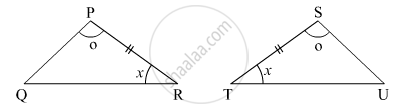
By ______ test
ΔPRQ ≅ ΔSTU
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: ΔAMC≅ ΔANB

State, whether the pairs of triangles given in the following figures are congruent or not:

In ΔABC and ΔPQR and, AB = PQ, BC = QR and CB and RQ are extended to X and Y respectively and ∠ABX = ∠PQY. = Prove that ΔABC ≅ ΔPQR.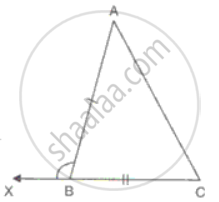
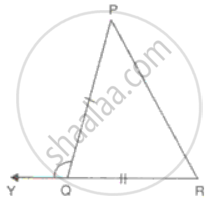
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.Prove that BO = CO and the ray AO is the bisector of angle BAC.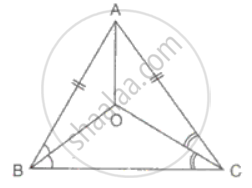
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.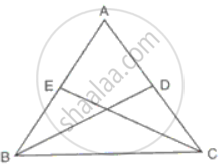
∆ABC and ∆PQR are congruent under the correspondence:
ABC ↔ RQP
Write the parts of ∆ABC that correspond to
(i) `bar"PQ"`
(ii)∠Q
(iii) `bar"RP"`
