Advertisements
Advertisements
प्रश्न
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is
विकल्प
100°
120°
110°
130°
उत्तर
Let ABCbe isosceles triangle
Then
AB = AC
∠B = ∠C
Now it is given that vertex angle is 2 times the sum of base angles
⇒∠A = 2 ∠(B+ C)
⇒∠A = 2 ∠(∠B + ∠B ) (As ∠B = ∠C)
⇒∠A = 2 (2∠B)
⇒∠A = 4 ∠B
Now
∠A + ∠B + ∠C = 180° (Property of triangle)
4∠B + ∠B + ∠B = 180° (Since ∠A = 4∠B, and ∠B = ∠C )
6∠B = 180°
∠B = 30°
∠A = 4∠B
`= 4 xx 30°`
= 120°
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠E
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) AM = AN (ii) ΔAMC ≅ ΔANB

State, whether the pairs of triangles given in the following figures are congruent or not:

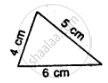
In the figure, ∠BCD = ∠ADC and ∠ACB =∠BDA. Prove that AD = BC and ∠A = ∠B.
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.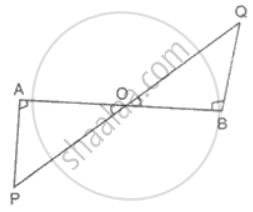
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.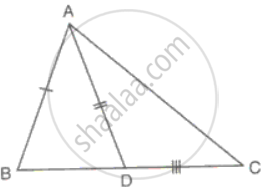
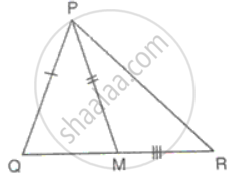
In ΔABC, AB = AC. D is a point in the interior of the triangle such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ΔABC.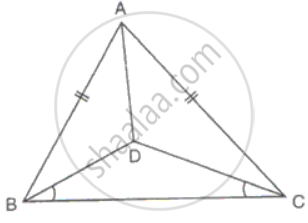
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆ABC ≅ ∆LMN
