Advertisements
Advertisements
प्रश्न
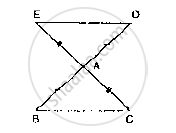
In Fig. 10.22, the sides BA and CA have been produced such that: BA = AD and CA = AE.
Prove that segment DE || BC.
उत्तर
Given that, the sides BA and CA have been produced such that BA =AD and CA= AE and
given to prove DE || BC
Consider triangle BAC and , DAE
We have
BA = ADand CA = AE [∵ given in the data]
And also ∠BAC=∠DAE [ ∵vertically opposite
angles]
So, by SAS congruence criterion, we have ΔBAC ≅ ΔDAE
⇒ BC = DE and ∠DEA=∠BCA, ∠EDA ∠CBA
[Corresponding parts of congruent triangles are equal]
Now, DE and BC are two lines intersected by a transversal DB such that ∠DEA =∠BCA,
i.e., alternate angles are equal
Therefore, DE || BC
APPEARS IN
संबंधित प्रश्न
In the following example, a pair of triangles is shown. Equal parts of triangles in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
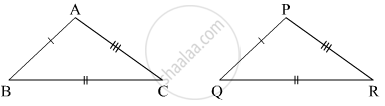
By ______ test
Δ ABC ≅ ΔPQR
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
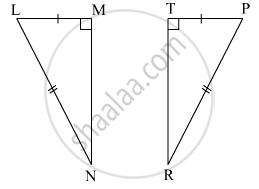
By ______ test
ΔLMN ≅ ΔPTR
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 8cm,BC = 6cm,∠B = 100°);
ΔPQR;(PQ = 8cm,RP = 5cm,∠Q = 100°).
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
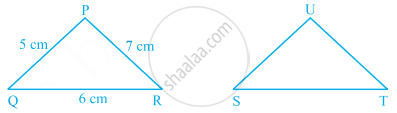
If ∆PQR is congruent to ∆STU (see figure), then what is the length of TU?