Advertisements
Advertisements
Question
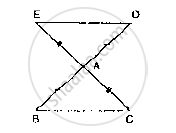
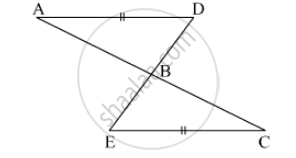
In Fig. 10.22, the sides BA and CA have been produced such that: BA = AD and CA = AE.
Prove that segment DE || BC.
Solution
Given that, the sides BA and CA have been produced such that BA =AD and CA= AE and
given to prove DE || BC
Consider triangle BAC and , DAE
We have
BA = ADand CA = AE [∵ given in the data]
And also ∠BAC=∠DAE [ ∵vertically opposite
angles]
So, by SAS congruence criterion, we have ΔBAC ≅ ΔDAE
⇒ BC = DE and ∠DEA=∠BCA, ∠EDA ∠CBA
[Corresponding parts of congruent triangles are equal]
Now, DE and BC are two lines intersected by a transversal DB such that ∠DEA =∠BCA,
i.e., alternate angles are equal
Therefore, DE || BC
APPEARS IN
RELATED QUESTIONS
In a squared sheet, draw two triangles of equal areas such that
The triangles are not congruent.
What can you say about their perimeters?
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that: LN = MN.
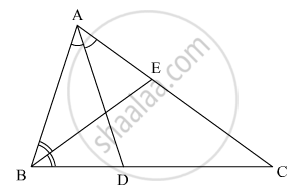
In the given figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that ADbisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.
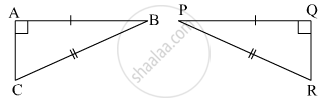
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.

In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
In the figure, BC = CE and ∠1 = ∠2. Prove that ΔGCB ≅ ΔDCE.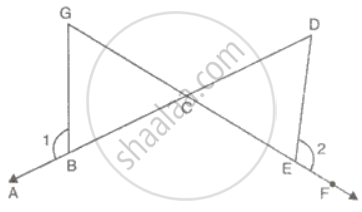
If AB = QR, BC = PR and CA = PQ, then ______.
