Advertisements
Advertisements
प्रश्न
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
उत्तर
We have to prove that the sum of three altitude of the triangle is less than the sum of its sides.
In ΔABC we have
AD ⊥BC,BE ⊥ AC and CF ⊥ AB
We have to prove
AD BE + CF < AB + BC + AC
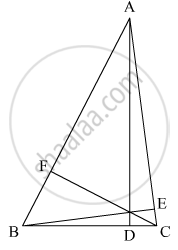
As we know perpendicular line segment is shortest in length
Since AD ⊥ BC
So AB >AD ........(1)
And
AC > AD ........(2)
Adding (1) and (2) we get
AB + AC > AD + AD
AB + AC > 2AD ........(3)
Now BE ⊥ AC, so
BC + BA > BE + BE
BC + BA > 2BE .......(4)
And againCF ⊥ AB , this implies that
AC + BC > 2AF ........(5)
Adding (3) & (4) and (5) we have
(AB + AC ) + (AB + BC )+ (AC + BC) >2AD + 2BE + 2CF
⇒ 2 (AB + BC + AC)>2(AD + BE + CF)
Hence AD BE + CF < AB + BC + AC Proved.
APPEARS IN
संबंधित प्रश्न
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
In a ΔABC, if AB = AC and BC is produced to D such that ∠ACD = 100°, then ∠A =
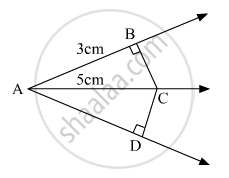
In the given figure, if AC is bisector of ∠BAD such that AB = 3 cm and AC = 5 cm, then CD =
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: ΔAMC≅ ΔANB

In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.Prove that BO = CO and the ray AO is the bisector of angle BAC.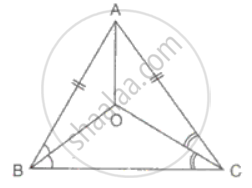
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
In ΔPQR, LM = MN, QM = MR and ML and MN are perpendiculars on PQ and PR respectively. Prove that PQ = PR.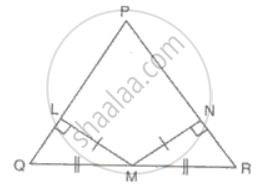
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
