Advertisements
Advertisements
Question
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
Solution
We have to prove that the sum of three altitude of the triangle is less than the sum of its sides.
In ΔABC we have
AD ⊥BC,BE ⊥ AC and CF ⊥ AB
We have to prove
AD BE + CF < AB + BC + AC
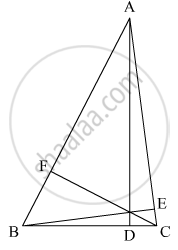
As we know perpendicular line segment is shortest in length
Since AD ⊥ BC
So AB >AD ........(1)
And
AC > AD ........(2)
Adding (1) and (2) we get
AB + AC > AD + AD
AB + AC > 2AD ........(3)
Now BE ⊥ AC, so
BC + BA > BE + BE
BC + BA > 2BE .......(4)
And againCF ⊥ AB , this implies that
AC + BC > 2AF ........(5)
Adding (3) & (4) and (5) we have
(AB + AC ) + (AB + BC )+ (AC + BC) >2AD + 2BE + 2CF
⇒ 2 (AB + BC + AC)>2(AD + BE + CF)
Hence AD BE + CF < AB + BC + AC Proved.
APPEARS IN
RELATED QUESTIONS
If ΔPQR≅ ΔEFD, then ∠E =
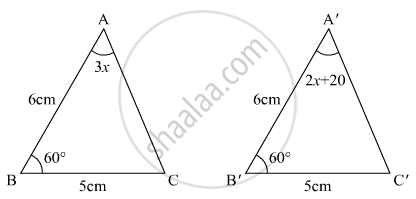
In the given figure, the measure of ∠B'A'C' is
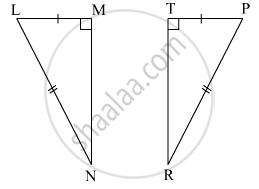
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

By ______ test
ΔXYZ ≅ ΔLMN
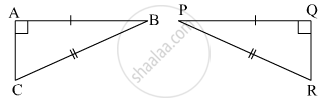
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
By ______ test
ΔLMN ≅ ΔPTR
From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.
If the following pair of the triangle is congruent? state the condition of congruency :
In ΔABC and ΔDEF, ∠B = ∠E = 90o; AC = DF and BC = EF.
In the given figure P is a midpoint of chord AB of the circle O. prove that OP ^ AB.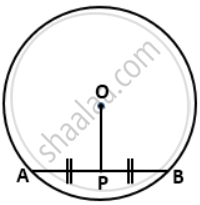
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.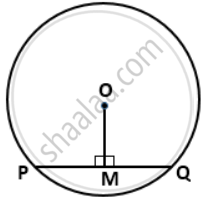
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.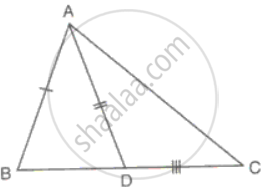
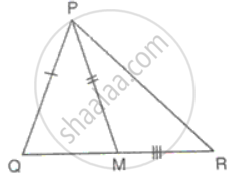
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side BC of ∆ABC so that the two triangles are congruent? Give reason for your answer.
