Question

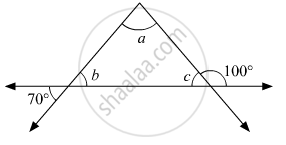
Using the information shown in figure, find the measures of ∠a, ∠b and ∠c.

Answer 1

∠c + 100^∘ = 180^∘       ...(Linear angle property)

∠c = 180^∘ - 100^∘

⇒ ∠c = 80^∘

Now, ∠b = 70^∘     ...(Vertically opposite angles)      

∠a + ∠b + ∠c = 180^∘       ...(The sum of measures of angles of a triangle is 180°.)   

⇒ ∠a + 70^∘ + 80^∘ = 180^∘  

⇒ ∠a + 150^∘ = 180^∘ 

⇒ ∠a = 180^∘ - 150^∘

⇒ ∠a = 30^∘  

Hence, the values of a, b and c are 30^∘, 70^∘ and 80^∘ respectively.