Advertisements
Advertisements
प्रश्न
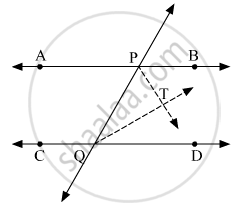
In the given Figure, line AB || line CD and line PQ is the transversal. Ray PT and ray QT are bisectors of ∠BPQ and ∠PQD respectively. Prove that m∠PTQ = 90°.
उत्तर
Given: line AB || line CD and line PQ is the transversal. Ray PT and ray QT are bisectors of ∠BPQ and ∠PQD respectively.
To prove: m∠PTQ = 90°
Proof:
∴ ∠TPB = ∠TPQ = `1/2∠"BPQ"` ...(i)[Ray PT bisects ∠BPQ]
∴ ∠TQD = ∠TQP = `1/2∠"PQD"` ...(ii)[Ray QT bisects ∠PQD]
line AB || line CD and line PQ is their transversal. ...(Given)
∴ ∠BPQ + ∠PQD = 180∘ ...[Interior angles]
`1/2(∠"BPQ") + 1/2(∠"PQD") = 1/2 × 180° ...["Multiplying both sides by" 1/2]`
∠TPQ + ∠TQP = 90° ...(iii)
In ΔPTQ,
∠TPQ + ∠TQP + ∠PTQ = 180° ...[Sum of the measures of the angles of a triangle is 180°]
∴ 90° + ∠PTQ = 180° ...[From (iii)]
∴ ∠PTQ = 180° − 90°
∴ ∠PTQ = 90°
∴ m∠PTQ = 90°
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the given figure, ∠ACD is an exterior angle of ΔABC. ∠B = 40°, ∠A = 70°. Find the measure of ∠ACD.

In ΔPQR, ∠P = 70°, ∠Q = 65° then find ∠R.
The measures of angles of a triangle are x°, (x - 20)°, (x - 40)°. Find the measure of each angle.
The measure of one of the angles of a triangle is twice the measure of its smallest angle and the measure of the other is thrice the measure of the smallest angle. Find the measures of the three angles.
In the given figure, measures of some angles are given. Using the measures find the values of x, y, z.

In the given figure, line AB || line DE. Find the measures of ∠DRE and ∠ARE using given measures of some angles.

In Δ ABC, bisectors of ∠A and ∠B intersect at point O. If ∠C = 70°. Find the measure of ∠AOB.
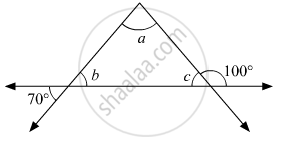
Using the information shown in figure, find the measures of ∠a, ∠b and ∠c.
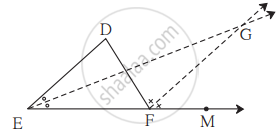
In the given figure, line DE || line GF, ray EG and ray FG are bisectors of ∠DEF and ∠DFM respectively. Prove that,
- ∠DEG = `1/2∠"EDF"`
- EF = FG