Advertisements
Advertisements
प्रश्न
In ΔPQR, ∠Q = 90°, PQ = 12, QR = 5 and QS is a median. Find l(QS).
उत्तर
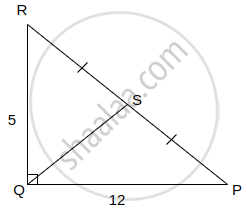
In △PQR, ∠Q = 90° ...[Given]
△PQR is a right angle triangle.
∴ By Pythagoras theorem,
∴ PR2 = PQ2 + QR2
⇒ PR2 = 122 + 52
⇒ PR2 = 144 + 25
⇒ PR2 = 169
⇒ PR = `sqrt169`
⇒ PR = 13
In △PQR,
seg QS is the median on hypotenuse PR.
∴ QS = `1/2`PR ...[In a right angled triangle, the length of the median on the hypotenuse is half the length of the hypotenuse.]
∴ QS = `1/2 × 13`
∴ QS = 6.5 units
Hence, the length of QS is 6.5 units.
APPEARS IN
संबंधित प्रश्न
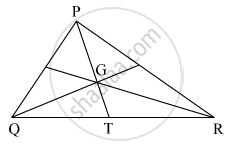
In the given figure, point G is the point of concurrence of the medians of Δ PQR. If GT = 2.5, find the lengths of PG and PT.
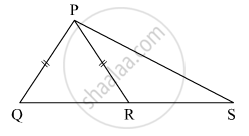
In the given figure, if seg PR ≅ seg PQ, show that seg PS > seg PQ.
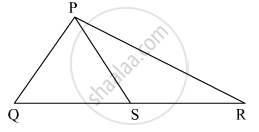
In the given figure, point S is any point on side QR of ΔPQR Prove that: PQ + QR + RP > 2PS
Draw an obtuse angled Δ STV. Draw its medians and show the centroid.
Draw an obtuse angled Δ LMN. Draw its altitudes and denote the orthocentre by ‘O’.
Draw an isosceles triangle. Draw all of its medians and altitudes. Write your observation about their points of concurrence.
The medians of a triangle cross each other at _______
The centroid of a triangle divides each medians in the ratio _______
The centroid, orthocentre, and incentre of a triangle are collinear
In ∆ABC, AD is the bisector of ∠A meeting BC at D, CF ⊥ AB and E is the mid-point of AC. Then median of the triangle is ______.
