Advertisements
Advertisements
प्रश्न
In ΔPQR, ∠Q = 90°, PQ = 12, QR = 5 and QS is a median. Find l(QS).
उत्तर
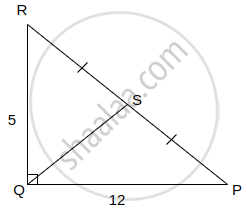
In △PQR, ∠Q = 90° ...[Given]
△PQR is a right angle triangle.
∴ By Pythagoras theorem,
∴ PR2 = PQ2 + QR2
⇒ PR2 = 122 + 52
⇒ PR2 = 144 + 25
⇒ PR2 = 169
⇒ PR = `sqrt169`
⇒ PR = 13
In △PQR,
seg QS is the median on hypotenuse PR.
∴ QS = `1/2`PR ...[In a right angled triangle, the length of the median on the hypotenuse is half the length of the hypotenuse.]
∴ QS = `1/2 × 13`
∴ QS = 6.5 units
Hence, the length of QS is 6.5 units.
APPEARS IN
संबंधित प्रश्न
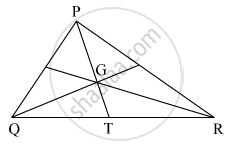
In the given figure, point G is the point of concurrence of the medians of Δ PQR. If GT = 2.5, find the lengths of PG and PT.
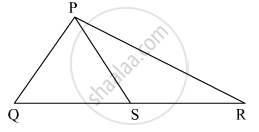
In the given figure, point S is any point on side QR of ΔPQR Prove that: PQ + QR + RP > 2PS
Draw an obtuse angled Δ LMN. Draw its altitudes and denote the orthocentre by ‘O’.
The medians of a triangle cross each other at _______
The centroid of a triangle divides each medians in the ratio _______
In any triangle the centroid and the incentre are located inside the triangle
The centroid, orthocentre, and incentre of a triangle are collinear
Identify the centroid of ∆PQR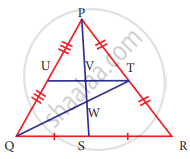
In the given figure, A is the midpoint of YZ and G is the centroid of the triangle XYZ. If the length of GA is 3 cm, find XA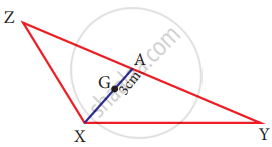
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If OE = 36 then EP = ?