Advertisements
Advertisements
प्रश्न
Draw an obtuse angled Δ LMN. Draw its altitudes and denote the orthocentre by ‘O’.
उत्तर
To draw an obtuse-angled ∆LMN.
i. Draw a base line of any length, mark it MN. At M draw an obtuse angle mark that line point L. Join L and N points. ΔLMN thus formed is an obtuse angled triangle.

ii. To draw an altitude from vertex L, extend side MN of the triangle from point M with a dashed line, as shown in the figure, and then draw the perpendicular lines from M.

iii. Considering side LN as a base, draw an altitude MP on side LN. Seg MP is an altitude on side LN.

iv. To draw altitude from vertex N, extend side LM of the triangle from point M with dashed line, as shown in the figure, and then draw the perpendicular line from vertex N.
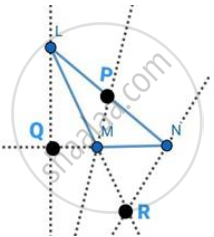
v. Now for the orthocentre, as all the altitudes do not intersect we'll have to extend them so that they can meet giving us an orthocentre of the triangle.
vi. Hence, extend the altitude LQ, from point Q ; MP from point M, and NR from point R.
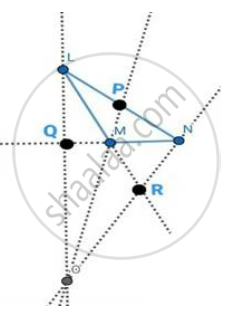
vii. The ortho centre of the Obtuse triangle lies outside the triangle.
viii. The point O denotes the orthocentre of the obtuse-angled ∆LMN.
संबंधित प्रश्न
In ΔPQR, ∠Q = 90°, PQ = 12, QR = 5 and QS is a median. Find l(QS).
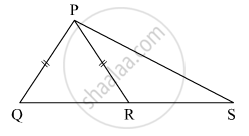
In the given figure, if seg PR ≅ seg PQ, show that seg PS > seg PQ.
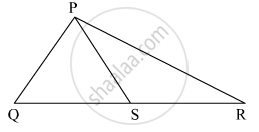
In the given figure, point S is any point on side QR of ΔPQR Prove that: PQ + QR + RP > 2PS
The medians of a triangle cross each other at _______
In any triangle the centroid and the incentre are located inside the triangle
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If DE = 44, then DM = ?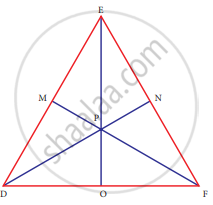
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If PD = 12, then PN = ?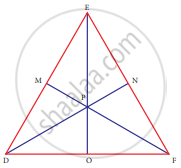
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If DO = 8, then FD = ?
In ∆ABC, AD is the bisector of ∠A meeting BC at D, CF ⊥ AB and E is the mid-point of AC. Then median of the triangle is ______.
If we join a vertex to a point on opposite side which divides that side in the ratio 1:1, then what is the special name of that line segment?
