Advertisements
Advertisements
प्रश्न
Draw an obtuse angled Δ STV. Draw its medians and show the centroid.
उत्तर

Steps of construction:
- Draw an obtuse, angled ∆ STV.
- Draw the perpendicular bisector AB of side TV that intersects side TV at L. L is the mid point of TV.
- Join SL, where SL is median to the side TV.
In the same manner, obtain the mid points M and N of sides SV and ST, respectively. - Join TM and VN.
Hence, ∆ STV is the required triangle in which the medians SL, TM and VN to the sides TV, SV and ST respectively intersect at point G.
The point G is the centroid of ∆ STV.
संबंधित प्रश्न
The length of hypotenuse of a right angled triangle is 15. Find the length of median of its hypotenuse.
In ΔPQR, ∠Q = 90°, PQ = 12, QR = 5 and QS is a median. Find l(QS).
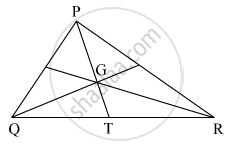
In the given figure, point G is the point of concurrence of the medians of Δ PQR. If GT = 2.5, find the lengths of PG and PT.
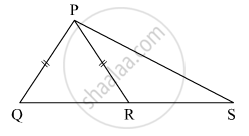
In the given figure, if seg PR ≅ seg PQ, show that seg PS > seg PQ.
The medians of a triangle cross each other at _______
In any triangle the centroid and the incentre are located inside the triangle
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If DE = 44, then DM = ?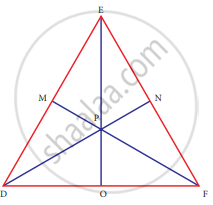
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If DO = 8, then FD = ?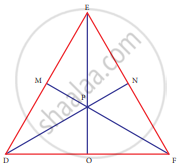
In ∆ABC, AD is the bisector of ∠A meeting BC at D, CF ⊥ AB and E is the mid-point of AC. Then median of the triangle is ______.
If we join a vertex to a point on opposite side which divides that side in the ratio 1:1, then what is the special name of that line segment?
