Advertisements
Advertisements
प्रश्न
In ∆ABC, AD is the bisector of ∠A meeting BC at D, CF ⊥ AB and E is the mid-point of AC. Then median of the triangle is ______.
विकल्प
AD
BE
FC
DE
उत्तर
In ∆ABC, AD is the bisector of ∠A meeting BC at D, CF ⊥ AB and E is the mid-point of AC. Then median of the triangle is BE.
Explanation:
As we know, the median of a triangle bisects the opposite sides.
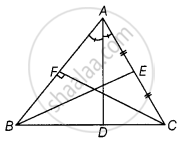
Hence, the median is BE as AE = EC.
APPEARS IN
संबंधित प्रश्न
In ΔPQR, ∠Q = 90°, PQ = 12, QR = 5 and QS is a median. Find l(QS).
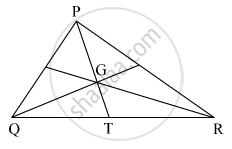
In the given figure, point G is the point of concurrence of the medians of Δ PQR. If GT = 2.5, find the lengths of PG and PT.
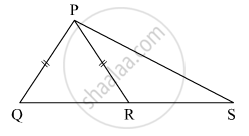
In the given figure, if seg PR ≅ seg PQ, show that seg PS > seg PQ.
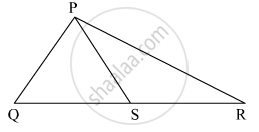
In the given figure, point S is any point on side QR of ΔPQR Prove that: PQ + QR + RP > 2PS
Draw an obtuse angled Δ LMN. Draw its altitudes and denote the orthocentre by ‘O’.
The centroid, orthocentre, and incentre of a triangle are collinear
Identify the centroid of ∆PQR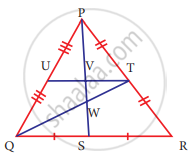
In the given figure, A is the midpoint of YZ and G is the centroid of the triangle XYZ. If the length of GA is 3 cm, find XA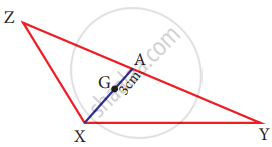
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following
If DE = 44, then DM = ?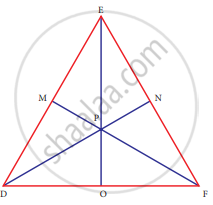
If we join a vertex to a point on opposite side which divides that side in the ratio 1:1, then what is the special name of that line segment?
