Advertisements
Advertisements
प्रश्न
If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is ______.
विकल्प
70°
110°
35°
145°
उत्तर
If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is 145°.
Explanation:
In ΔABC, ∠A = 110° .....[Given]
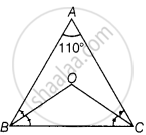
We know that, ∠A + ∠B + ∠C = 180° ......[Angle sum property of a triangle]
⇒ ∠B + ∠C = 180° – ∠A
⇒ ∠B + ∠C = 180° – 110°
⇒ ∠B + ∠C = 70° ......(i)
⇒ `1/2 ∠B + 1/2 ∠C = 70/2` = 35° ......[∵ Equation (i) is divided by 2]
⇒ `1/2 (∠B + ∠C)` = 35°
Now, In ΔBOC,
∠BOC + ∠OBC + ∠OCB = 180° [Angle sum property of a triangle] ......(ii)
⇒ `∠BOC + 1/2 (∠B + ∠C)` = 180° ......[∵ OB and OC are the bisectors of ∠B and ∠C, then ∠OBC = `1/2`∠B and ∠OCB = `1/2`∠C]
⇒ ∠BOC + 35° = 180°
⇒ ∠BOC = 180° – 35°
⇒ ∠BOC = 145°
APPEARS IN
संबंधित प्रश्न
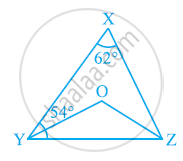
In the given figure, ∠X = 62º, ∠XYZ = 54º. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
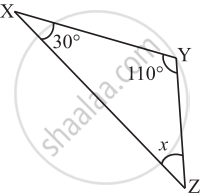
Find the value of the unknown x in the given diagram:
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B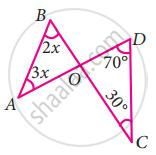
In ∆XYZ, if ∠X : ∠Z is 5 : 4 and ∠Y = 72°. Find ∠X and ∠Z
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
Prove that a triangle must have atleast two acute angles.
Triangle DEF of the given figure is a right triangle with ∠E = 90°. What type of angles are ∠D and ∠F?
If one angle of a triangle is equal to the sum of other two, then the measure of that angle is ______.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
