Advertisements
Advertisements
प्रश्न
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
उत्तर
Given ∠F = 48°
∠E = 68°
In ∆DEF,
∠D + ∠F + ∠E = 180° ...[By angle sum property]
∠D + 68° + 68° = 180°
∠D + 116° = 180°
∠D = 180° – 116°
= 64°
Since DG is the angular bisector of ∠D
∠FDG = ∠GDE
Also ∠FDG + ∠GDE = ∠D
2 ∠FDG = 64°
2 ∠FDG = 64°
∠FDG = `(64^circ)/2` = 32°
∠FDG = 32°
In ∆FDG,
∠FDG + ∠GFD = 180° ...[By angle sum property of triangles]
32° + ∠FDG + 48° = 180°
∠FDG + 80° = 180°
∠FDG = 180° – 80°
∠FDG = 100°
APPEARS IN
संबंधित प्रश्न
In the following triangle, find the value of x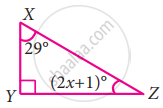
Observe the figure and find the value of ∠A + ∠N + ∠G + ∠L + ∠E + ∠S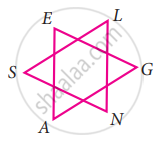
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
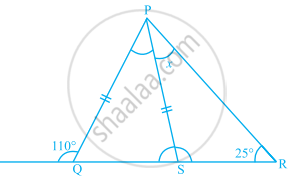
In the given figure, PQ = PS. The value of x is ______.
In a right-angled triangle, the angles other than the right angle are ______.
In the given figure, ∠BAC = 90°, AD ⊥ BC and ∠BAD = 50°, then ∠ACD is ______.

By which of the following criterion two triangles cannot be proved congruent?
I have three sides. One of my angle measures 15°. Another has a measure of 60°. What kind of a polygon am I? If I am a triangle, then what kind of triangle am I?
The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10°, find the three angles.
In the given figure, if ST = SU, then find the values of x and y.

