Advertisements
Advertisements
प्रश्न
In the following triangle, find the value of x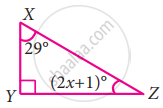
उत्तर
Let ∠Z = (2x + 1)° and ∠Y = 90°
By the sum property of triangle we have
∠x + ∠y + ∠z = 180°
29° + 90° + (2x + 1)° = 180°
119° + (2x + 1)° = 180°
(2x + 1)° = 180° – 119°
2x + 1° = 61°
2x = 61° – 1°
2x = 60°
x = `(60^circ)/2`
x = 30°
APPEARS IN
संबंधित प्रश्न
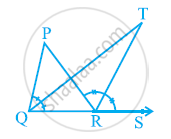
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B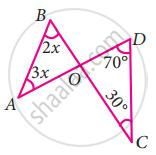
If the three angles of a triangle are in the ratio 3 : 5 : 4, then find them
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is ______.
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be ______.
Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is ______.
A triangle ABC is right angled at A. L is a point on BC such that AL ⊥ BC. Prove that ∠BAL = ∠ACB.
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
It is possible to have a triangle in which each angle is greater than 60°.
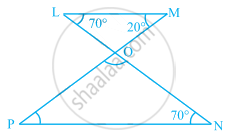
In the given figure, find the measures of ∠PON and ∠NPO.