Advertisements
Advertisements
प्रश्न
Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is ______.
विकल्प
60°
40°
80°
20°
उत्तर
Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is 40°.
Explanation:
Given, the ratio of angles of a triangle is 2 : 4 : 3.
Let the angles of a triangle be ∠A, ∠B and ∠C.
∠A = 2x, ∠B = 4x and ∠C = 3x ,
∠A + ∠B + ∠C = 180° ...[Sum of all the angles of a triangle is 180°]
2x + 4x + 3x = 180°
9x = 180°
x = `(180^circ)/9` = 20°
∠A = 2x = 2 × 20° = 40°
∠B = 4x = 4 × 20° = 80°
∠C = 3x = 3 × 20° = 60°
Hence, the smallest angle of a triangle is 40°.
APPEARS IN
संबंधित प्रश्न
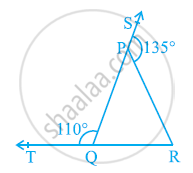
In the given figure, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135º and ∠PQT = 110º, find ∠PRQ.
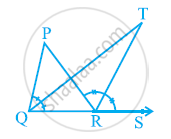
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
In the following triangle, find the value of x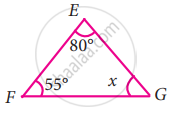
In the following triangle, find the value of x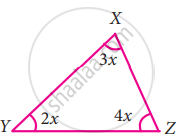
In the following triangle, find the value of x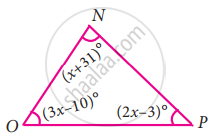
If one angle of a triangle is equal to the sum of the other two angles, the triangle is ______.
In the given figure, find the values of a, b and c.
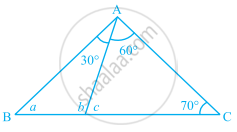
In the given figure, find the values of a, b and c
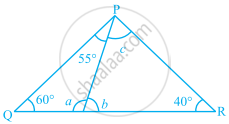
Find the values of x and y in the given figure.
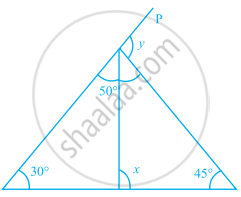
The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10°, find the three angles.
