Advertisements
Advertisements
प्रश्न
In the following figure, if OP || RS, ∠OPQ = 110° and ∠QRS = 130°, then ∠PQR is equal to ______.

विकल्प
40°
50°
60°
70°
उत्तर
In the following figure, if OP || RS, ∠OPQ = 110° and ∠QRS = 130°, then ∠PQR is equal to 60°.
Explanation:
See the given figure, producing OP, to intersect RQ at X.
Given: OP || RS and RX is a transversal.
So, ∠RXP = ∠XRS ...(Alternative angle)
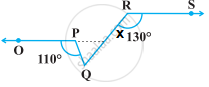
∠RXP = 130° ...[Given: ∠QRS = 130°]
RQ is a line segment.
So, ∠PXQ + ∠RXV = 180° ...[Linear pair axiom]
∠PXQ = 180° – ∠RXP = 180° – 130°
∠PXQ = 50°
In triangle PQX, ∠OPQ is an exterior angle,
Therefore, ∠OPQ = ∠PXQ + ∠PQX ...[Exterior angle = Sum of two opposite angles]
110° = 50° + ∠PQX
∠PQX = 110° – 50°
∠PQR = 60°
APPEARS IN
संबंधित प्रश्न
If two straight lines are perpendicular to the same line, prove that they are parallel to each
other.
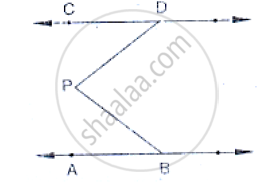
In the below fig, lines AB and CD are parallel and P is any point as shown in the figure.
Show that` ∠`ABP +` ∠`CDP = ∠DPB.
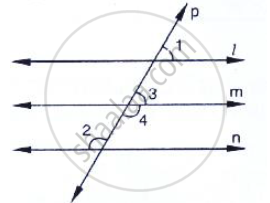
In the below fig, if l || m || n and `∠`1 = 60°, find `∠`2.
Which of the following statement are true and false ? Give reason.
If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
Fill in the blank in the following to make the statement true:
If a transversal intersects a pair of lines in such a way that a pair of alternate angles
are equal, then the lines are _______
Fill in the blank :
If a transversal intersects a pair of lines in such a way that the sum of interior angles
on the same side of transversal is 180°, then the lines are _______.
If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2:3, then the measure of the larger angle is
In the given figure, if lines l and m are parallel, then the value of x is

Two lines l and m are perpendicular to the same line n. Are l and m perpendicular to each other? Give reason for your answer.
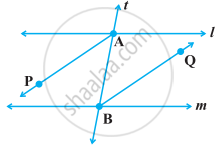
AP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (Figure). Show that AP || BQ.