Advertisements
Advertisements
рдкреНрд░рд╢реНрди
If two straight lines are perpendicular to the same line, prove that they are parallel to each
other.
рдЙрддреНрддрд░
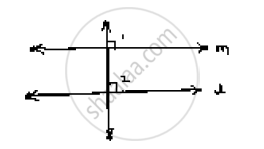
Given m perpendicular ЁЭСб and l ⊥ t
`∠`1 = `∠`2 = 90°
∴ l and m are two lines and it is transversal and the corresponding angles are equal
∴ l || m
Hence proved
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
In the below fig, l, m and n are parallel lines intersected by transversal p at X, Y and Z
respectively. Find ∠1, ∠2 and ∠3.
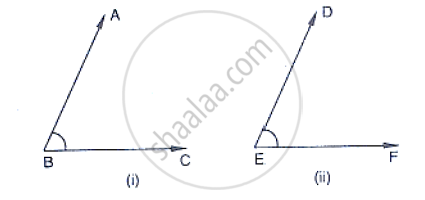
In the below fig, arms BA and BC of `∠`ABC are respectively parallel to arms ED and EF of
`∠`DEF. Prove that `∠`ABC = ∠DEF.
Which of the following statement are true and false ? Give reason.
If two parallel lines are intersected by a transversal, then the interior angles on the same side of the transversal are equal.
In the given figure, if lines l and m are parallel, then x =
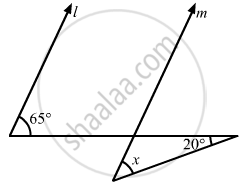
In the given figure, if lines l and m are parallel lines, then x =
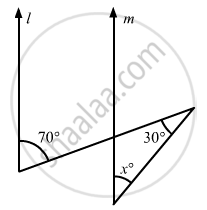
In the given figure, if l || m, then x =
In the given figure, if \[\frac{y}{x} = 5\] and \[\frac{z}{x} = 4\] then the value of x isc
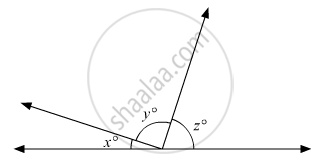
In the given figure, If line segment AB is parallel to the line segment CD, what is the value of y?
Two lines l and m are perpendicular to the same line n. Are l and m perpendicular to each other? Give reason for your answer.
A transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel.
