Advertisements
Advertisements
Question
If two straight lines are perpendicular to the same line, prove that they are parallel to each
other.
Solution
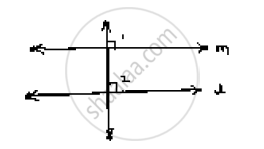
Given m perpendicular 𝑡 and l ⊥ t
`∠`1 = `∠`2 = 90°
∴ l and m are two lines and it is transversal and the corresponding angles are equal
∴ l || m
Hence proved
APPEARS IN
RELATED QUESTIONS
In the below fig, AB || CD || EF and GH || KL. Find `∠`HKL
Which pair of lines in the below fig, is parallel? Given reasons.

Fill in the blank in the following to make the statement true:
If two parallel lines are intersected by a transversal, then interior angles on the same
side of the transversal are _______
In the given figure, if l1 || l2, what is the value of y?
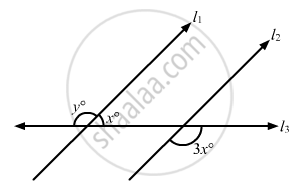
In the given figure, if lines l and m are parallel, then the value of x is

In the given figure, If line segment AB is parallel to the line segment CD, what is the value of y?

In the following figure, find the value of x for which the lines l and m are parallel.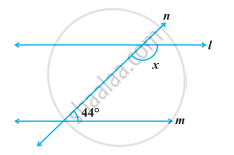
In the following figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l ||m.
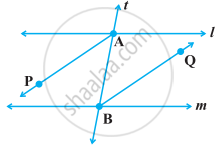
In the following figure, BA || ED and BC || EF. Show that ∠ABC = ∠DEF
[Hint: Produce DE to intersect BC at P (say)].
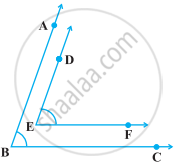
In the following figure, BA || ED and BC || EF. Show that ∠ABC + ∠DEF = 180°