Advertisements
Advertisements
Question
In the given figure, if lines l and m are parallel, then the value of x is

Options
35°
55°
65°
75°
Solution
The given figure is as follows with : l || m
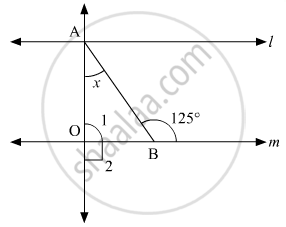
Also, ∠1 and ∠2 form a linear pair. Thus,
∠1 +∠2 = 180°
It is given that ∠2 = 90°, substituting this value , we get :
∠1 + 90° = 180°
∠1 = 180° - 190°
∠1 = 90° (i)
In a triangle, we know that, the exterior angle is equal to the sum of the interior opposite angle.
In ΔAOB:
x + ∠1 = 125°
x = 125° - ∠1
From equation (i):
x = 125° - 90°
x = 35°
APPEARS IN
RELATED QUESTIONS
Which pair of lines in the below fig, is parallel? Given reasons.

Which of the following statement are true and false ? Give reason.
If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
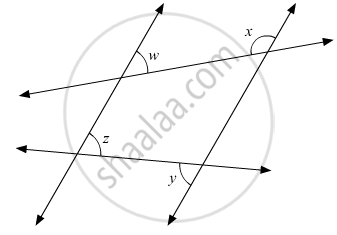
In the given figure, if l1 || l2, what is x + y in terms of w and z?
In the given figure, if AB || CD, then x =

In the given figure, if \[\frac{y}{x} = 5\] and \[\frac{z}{x} = 4\] then the value of x isc
AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠FEB. If ∠LEB = 35°, then ∠CFQ will be
In the following figure, if OP || RS, ∠OPQ = 110° and ∠QRS = 130°, then ∠PQR is equal to ______.

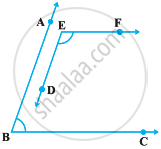
In the following figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l ||m.
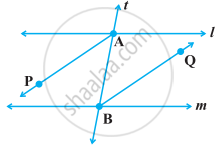
In the following figure, BA || ED and BC || EF. Show that ∠ABC = ∠DEF
[Hint: Produce DE to intersect BC at P (say)].
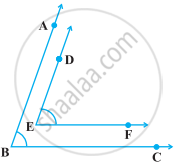
In the following figure, BA || ED and BC || EF. Show that ∠ABC + ∠DEF = 180°