Parallel Lines and a Transversal

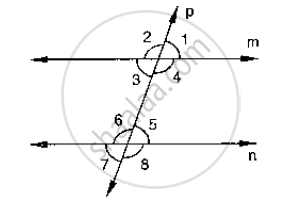
A line which intersects two or more lines at distinct points is called a transversal in following fig .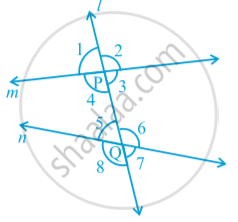

Line l intersects lines m and n at points P and Q respectively. Therefore, line l is a transversal for lines m and n. Observe that four angles are formed at each of the points P and Q. Let us name these angles as ∠ 1, ∠ 2, . . ., ∠8 as shown in above  Fig. 
∠ 1, ∠ 2, ∠ 7 and ∠ 8 are called exterior angles, while ∠ 3, ∠ 4, ∠ 5 and ∠ 6 are called interior angles. 
Some pairs of angles formed when a transversal intersects two lines. These are as follows:
(a) Corresponding angles :
(i) ∠ 1 and ∠ 5 (ii) ∠ 2 and ∠ 6
(iii) ∠ 4 and ∠ 8 (iv) ∠ 3 and ∠ 7

(b) Alternate interior angles :
(i) ∠ 4 and ∠ 6 (ii) ∠ 3 and ∠ 5

(c) Alternate exterior angles:
(i) ∠ 1 and ∠ 7 (ii) ∠ 2 and ∠ 8

(d) Interior angles on the same side of the transversal:
(i) ∠ 4 and ∠ 5 (ii) ∠ 3 and ∠ 6

Interior angles on the same side of the transversal are also referred to as consecutive interior angles or allied angles or co-interior angles.

Axiom: If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.
Axiom  is also referred to as the corresponding angles axiom.
If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel.
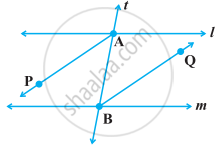
It can be verified as follows: Draw a line AD and mark points B and C on it. At B and C, construct ∠ ABQ and ∠ BCS equal to each other as shown in Fig.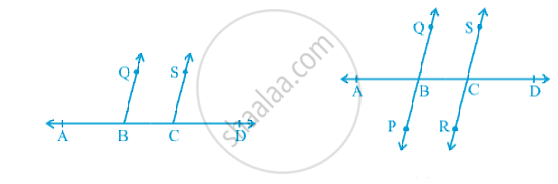

Produce QB and SC on the other side of AD to form two lines PQ and RS . You may observe that the two lines do not intersect each other. You may also draw common perpendiculars to the two lines PQ and RS at different points and measure their lengths. Therefore, the converse of corresponding angles axiom is also true. 

Axiom:  If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel to each other.
The relation between the alternate interior angles when a transversal intersects two parallel lines ? in fig. 

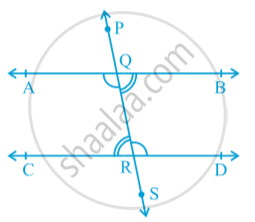
transveral PS intersects parallel lines AB and CD at points Q and R respectively.  
Is ∠ BQR = ∠ QRC and ∠ AQR = ∠ QRD? 
You know that ∠ PQA = ∠ QRC (1) (Corresponding angles axiom)
Is ∠ PQA = ∠ BQR   (2)
So, from (1) and (2), you may conclude that
∠ BQR = ∠ QRC.
Similarly, ∠ AQR = ∠ QRD.

Theorem:   If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal. 

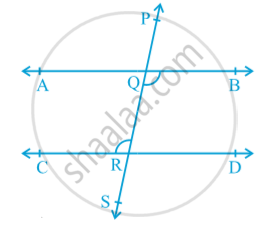
In above fig.  the transversal PS intersects lines AB and CD at points Q and R respectively such that ∠ BQR = ∠ QRC.
Is AB || CD 
∠ BQR = ∠ PQA   (1)
But, ∠ BQR = ∠ QRC (Given) (2)
So, from (1) and (2), you may conclude that
∠ PQA = ∠ QRC
But they are corresponding angles.
So, AB || CD (Converse of corresponding angles axiom)

Theorem: If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel. 

Theorem: If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.

Theorem: If a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.