Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
- Introduction
- Convention for Measuring Area
Introduction
The area of a closed shape is the total surface it covers, measured in terms of the number of unit squares enclosed within its boundary.
It is expressed in square units (e.g., square centimeters, square meters, square inches, etc.)
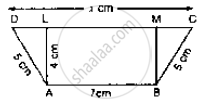
Example: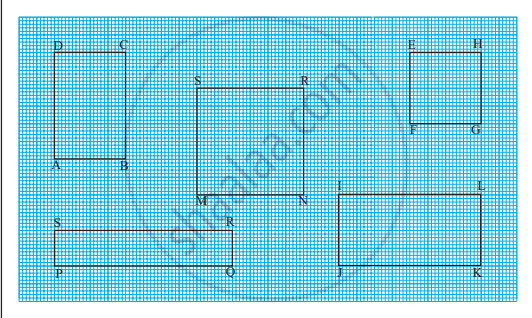
Of the figures given above, figure ABCD has six squares of 1 cm each inside it. It means that its area is 6 sq cm.
In the same way, count the squares in each figure and write its area.
(1) Area of MNRS = 9 sq cm
(2) Area of EFGH = 4 sq cm
(3) Area of PQRS = 5 sq cm
(4) Area of IJKL = 8 sq cm
Convention for Measuring Area
In some instances, squares may not fit exactly into the measured area. To address this issue, the following convention is adopted:
1. The area of one entire square is considered as 1 square unit:
- If using a square centimetre sheet, the area of one entire square is 1 square centimetre (1 sq cm).
2. Handling Partial Squares:
- Portions of the area that are less than half of a square are ignored.
- If more than half of a square falls within the measured region, it is counted as one full square.
- If exactly half of a square is included, its area is considered as `1/2` square units.

| Covered area | Number | Area estimate (sq. units) |
| (i) Fully-filled squares | 101 | 101 |
| (ii) Half-filled squares | 4 | 4 × `1/2` |
| (iii) More than half-filled squares | 21 | 21 |
| (iv) Less than half-filled squares | 23 | 0 |
Total area = 101 + 4 × `1/2` + 21 = 126`1/2` sq. Units.
Example
By counting squares, estimate the area of the figure.

| Covered area | Number |
Area estimate |
| (i) Fully-filled squares | 11 | 11 |
| (ii) Half-filled squares | 3 | `3 xx 1/2` |
| (iii) More than half-filled squares | 7 | 7 |
| (iv) Less than half-filled squares | 5 | 0 |
Total area = 11 + 3 × `1/2 + 7 = 19 1/2` sq units.
Example
By counting squares, estimate the area of the figure.

| Covered area | Number | Area estimate (sq units) |
| (i) Fully-filled squares | 1 | 1 |
| (ii) Half-filled squares | - | - |
| (iii) More than half-filled squares | 7 | 7 |
| (iv) Less than half-filled squares | 9 | 0 |
Total area = 1 + 7 = 8 sq units.