Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
Text
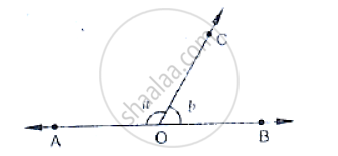
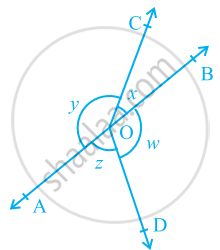
Axiom : If a ray stands on a line, then the sum of two adjacent angles so formed is 180°.
The sum of two adjacent angles is 180°, then they are called a linear pair of angles. It is given that ‘a ray stands on a line’. From this ‘given’, we have concluded that ‘the sum of two adjacent angles so formed is 180°’.
The ‘conclusion’ of Axiom as ‘given’ and the ‘given’ as the ‘conclusion’. So it becomes:
(A) If the sum of two adjacent angles is 180°, then a ray stands on a line (that is, the non-common arms form a line).
The Axiom and statement (A) are in a sense the reverse of each others. We call each as converse of the other.
Axiom: If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line. For obvious reasons, the two axioms above together is called the Linear Pair Axiom. Two lines intersect, the vertically opposite angles are equal.
Theorem
Theorem: If two lines intersect each other, then the vertically opposite angles are equal.
Proof : In the statement above, it is given that ‘two lines intersect each other’. So, let AB and CD be two lines intersecting at O as shown in Fig. 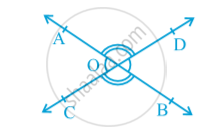
They lead to two pairs of vertically opposite angles, namely,
(i) ∠ AOC and ∠ BOD (ii) ∠ AOD and ∠ BOC.
We need to prove that ∠ AOC = ∠ BOD and ∠ AOD = ∠ BOC.
Now, ray OA stands on line CD.
Therefore, ∠ AOC + ∠ AOD = 180° (Linear pair axiom) (1)
Can we write ∠ AOD + ∠ BOD = 180° (2)
From (1) and (2), we can write
∠ AOC + ∠ AOD = ∠ AOD + ∠ BOD
This implies that ∠ AOC = ∠ BOD
Similarly, it can be proved that ∠AOD = ∠BOC.