Advertisements
Advertisements
Question
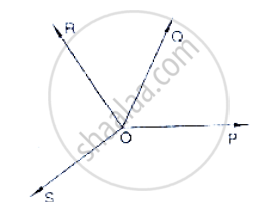
In below fig, OP, OQ, OR and OS arc four rays. Prove that:
∠POQ + ∠QOR + ∠SOR + ∠POS = 360°
Solution
Given that
OP, OQ, OR and OS are four rays
You need to produce any of the ray OP, OQ, OR and OS backwards to a point in the figure. Let us produce ray OQ backwards to a point
T so that TOQ is a line
Ray OP stands on the TOQ
Since `∠`TOP, `∠`POQ is linear pair
`∠`TOP + `∠`POQ = 180° .......(1)
Similarly, ray OS stands on the line TOQ
∴`∠`TOS + `∠`SOQ = 180° ..........(2)
But `∠`SOQ = `∠`SOR + `∠`QOR
So, (2), becomes
`∠`TOS + `∠`SOR + `∠`OQR = 180°
Now, adding (1) and (3) you get
`∠`TOP + `∠`POQ + `∠`TOS + `∠`SOR + `∠`QOR = 360°
⇒ `∠`TOP + `∠`TOS = `∠`POS
∴ (4) becomes
`∠`POQ + `∠`QOR + `∠`SOR + `∠`POS = 360°
APPEARS IN
RELATED QUESTIONS
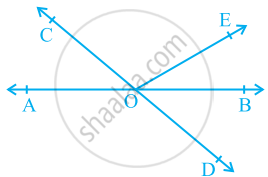
In the given figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
Write the complement of the following angle.
20°
Write the complement of the following angles.
77°
Write the complement of the following angles .
30°
Two supplementary angles differ by 48°. Find the angles.
An angle is equal to 8 times its complement. Determine its measure.
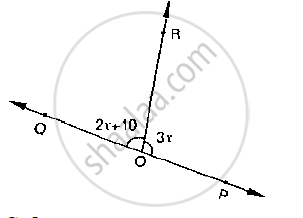
Given ∠POR = 3x and ∠QOR = 2x + 10, find the value of x for which POQ will be a line.
(Below fig).
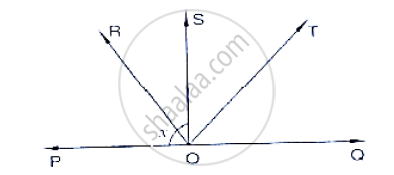
In below fig, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS
and ∠SOQ respectively. If ∠POS = x, find ∠ROT.
In the below fig, find the value of x.

statement are true and false
Angles forming a linear pair are supplementary.
