Advertisements
Advertisements
Question
Two supplementary angles differ by 48°. Find the angles.
Solution
Given that two supplementary angles are differ by 48°
Let the angle measured is x°
∴ Its supplementary angle will be (180 - x)°
It is given that
(180 - x) - x = 98°
⇒ 180 - 48° = 2x
⇒ 132 = 2x
⇒ x = `132/2`
⇒ x = 66°
Hence, 180 - x = 114°
Therefore, angles are 66° and 114°
APPEARS IN
RELATED QUESTIONS
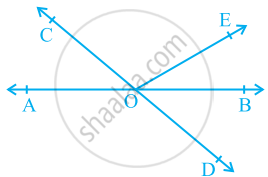
In the given figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
If the supplement of an angle is three times its complement, find the angle.
If the supplement of an angle is two-third of itself. Determine the angle and its supplement.
The measure of an angle is twice the measure of its supplementary ang Find its measure.
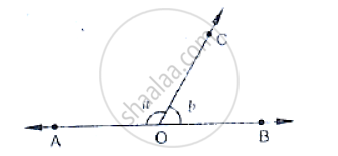
In the below fig, write all pairs of adjacent angles and all the linear pairs .

In the below Fig, ∠AOC and ∠BOC form a linear pair. if a − 2b = 30°, find a and b.
In the below fig, AOC is a line, find x.
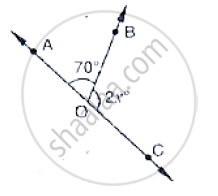
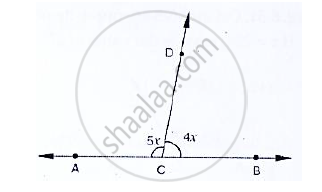
In the below fig, ACB is a line such that ∠DCA = 5x and ∠DCB = 4x. Find the value of x.
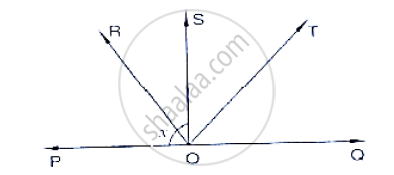
In below fig, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS
and ∠SOQ respectively. If ∠POS = x, find ∠ROT.
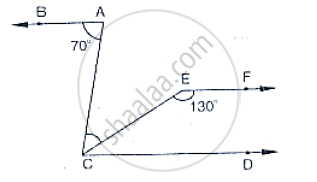
If below fig, if AB || CD and CD || EF, find ∠ACE.