Advertisements
Advertisements
Question
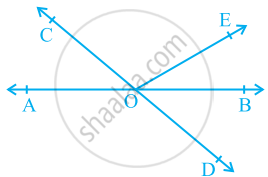
In the given figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
Solution
AB is a straight line, and rays OC and OE stand on it.
∴ ∠AOC + ∠COE + ∠BOE = 180°
⇒ (∠AOC + ∠BOE) + ∠COE = 180°
⇒ 70° + ∠COE = 180°
⇒ ∠COE = 180° − 70° = 110°
Reflex ∠COE = 360° − 110° = 250°
The CD is a straight line, and rays OE and OB stand on it.
∴ ∠COE + ∠BOE + ∠BOD = 180°
⇒ 110° + ∠BOE + 40° = 180°
⇒ ∠BOE = 180° − 150° = 30°
Thus, ∠BOE = 30° and reflex ∠COE = 250°
APPEARS IN
RELATED QUESTIONS
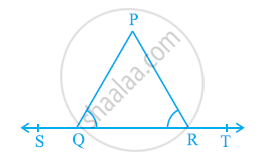
In the given figure, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
Write the complement of the following angles.
90°
Two supplementary angles are in the ratio 4 : 5. Find the angles.
If the complement of an angle is equal to the supplement of the thrice of it. Find the measure of the angle.
If the supplement of an angle is two-third of itself. Determine the angle and its supplement.
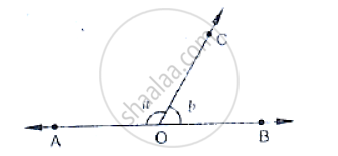
In the below Fig, ∠AOC and ∠BOC form a linear pair. if a − 2b = 30°, find a and b.
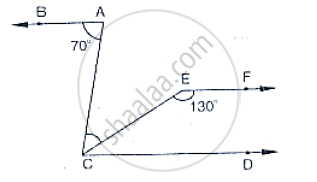
If below fig, if AB || CD and CD || EF, find ∠ACE.
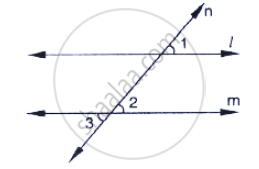
In the below fig, `∠`1 = 60° and `∠`2 = `(2/3)^(rd)`of a right angle. Prove that l || m.
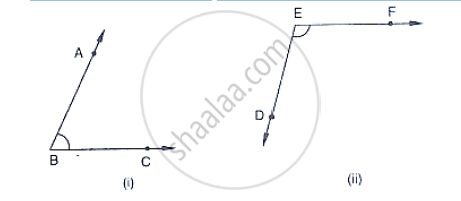
In the below fig, arms BA and BC of ∠ABC are respectively parallel to arms ED and EF of
∠DEF. Prove that ∠ABC + ∠DEF = 180°.
Fill in the blank in the following to make the statement true:
If two parallel lines are intersected by a transversal, then each pair of corresponding
angles are _______
