Advertisements
Advertisements
प्रश्न
In below fig, OP, OQ, OR and OS arc four rays. Prove that:
∠POQ + ∠QOR + ∠SOR + ∠POS = 360°
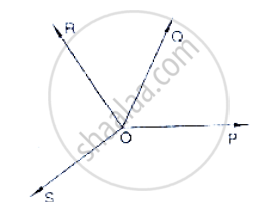
उत्तर
Given that
OP, OQ, OR and OS are four rays
You need to produce any of the ray OP, OQ, OR and OS backwards to a point in the figure. Let us produce ray OQ backwards to a point
T so that TOQ is a line
Ray OP stands on the TOQ
Since `∠`TOP, `∠`POQ is linear pair
`∠`TOP + `∠`POQ = 180° .......(1)
Similarly, ray OS stands on the line TOQ
∴`∠`TOS + `∠`SOQ = 180° ..........(2)
But `∠`SOQ = `∠`SOR + `∠`QOR
So, (2), becomes
`∠`TOS + `∠`SOR + `∠`OQR = 180°
Now, adding (1) and (3) you get
`∠`TOP + `∠`POQ + `∠`TOS + `∠`SOR + `∠`QOR = 360°
⇒ `∠`TOP + `∠`TOS = `∠`POS
∴ (4) becomes
`∠`POQ + `∠`QOR + `∠`SOR + `∠`POS = 360°
APPEARS IN
संबंधित प्रश्न
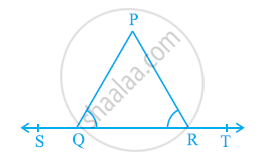
In the given figure, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
If an angle differs from its complement by 10°, find the angle .
An angle is 14° more than its complementary angle. What is its measure?
The measure of an angle is twice the measure of its supplementary ang Find its measure.
In the below Fig, OA and OB are opposite rays.
If y = 35°, what is the value of x?
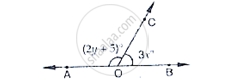
In Fig. 8.42, a is greater than b by one third of a right-angle. Find the values of a and b.
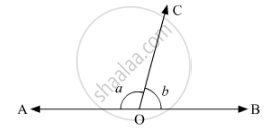
statement are true and false
Angles forming a linear pair are supplementary.
If below fig, if AB || CD and CD || EF, find ∠ACE.
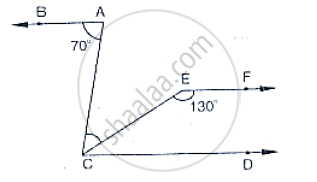
In the below fig, `∠`1 = 60° and `∠`2 = `(2/3)^(rd)`of a right angle. Prove that l || m.
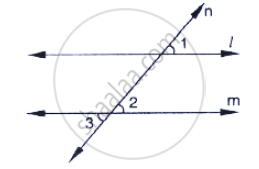
If two lines intersect, prove that the vertically opposite angles are equal.
